Dopo il primo, ecco il secondo post di Paolo sul calcolo delle probabilità.
Probabilità di eventi che si presentano in casi egualmente possibili
Se l'evento E si presenta in un certo numero di casi (n), tutti egualmente possibili e, di questi, solo una parte (m) sono favorevoli a E, la probabilità che si presenti l'evento favorevole è data dalla formula:
P(E)=m/n
Più precisamente, la probabilità di un evento è misurata dal rapporto fra il numero dei casi favorevoli all'evento ed il numero dei casi egualmente possibili.
In pratica, se considero l'esempio di un'urna contenente 100 palline di cui metà bianche e metà nere, la probabilità di estrarre una pallina bianca è data dalla formula
P(E)=50/100, ovvero 0,50 che equivale al 50%. Cioè la probabilità di estrarre una pallina bianca è pari al 50%.
Analogamente circa la probabilità di estrarre una pallina nera.
Per contro, se l'urna contenesse 25 palline bianche e 75 nere, la probabilità di estrarre una pallina bianca sarebbe
P(E)=25/100, ovvero 0,25 che equivale al 25%.
In questo caso, la probabilità di estrarre una pallina nera diventerebbe
P(E)=75/100, cioè 75%.
Da questo esempio si possono estrapolare due importanti postulati:
• il primo, già citato, che la probabilità di un evento è sempre compresa fra 0 e 1 con esclusione degli estremi;
• il secondo che la probabilità del NON evento E, ovvero che non si verifichi l'evento, è data dalla differenza 1- P(E);
nel caso esemplificato la probabilità di estrarre una pallina nera è data da 1-25%, appunto 75%.
Il lancio di una moneta
rappresenta un altro esempio significativo:
la probabilità che si presenti il lato testa o, viceversa, il lato croce è pari al 50% in quanto vi è un solo evento favorevole su 2 casi egualmente possibili.
Quando si parla di casi egualmente possibili significa che le condizioni in cui i questi si presentano devono essere identiche.
Nell'esempio citato, le palline sono identiche sotto tutti gli aspetti, tranne il colore. Sono quindi perfettamente sferiche, della stessa materia, dello stesso peso e dimensione e così via.
Così pure la moneta deve essere perfettamente equilibrata, avere le facce con rilievo non distinguibile e quant'altro.
Se così non fosse si invaliderebbe il principio di casualità, che sta alla base del calcolo delle probabilità.
E ora un piccolo esercizio (da internet):
Disponi di due urne da cui devi estrarre casualmente una pallina. Quale sceglieresti se il premio si ottiene estraendo il nero?
Post
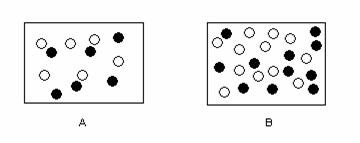
Ritengo che sia indifferente la scelta dell' urna. La probabilita' che si estragga una pallina nera dall' urna A e identica a quella dell' urna B, sino a che non si precisa se, scegliendo l' una o altra urna, l' estrazione e' unica oppure no. Se l' estrazione non fosse unica bisognerebbe poi specificare se, nella seconda estrazione, la pallina estratta viene rimessa nell' urna oppure no.
RispondiEliminaCiao Giovanna passo per un saluto e per augurarti buon anno scolastico. Sul mio blog ho scritto un pensiero .
RispondiEliminaun abbraccio grande
eheh... bello! ;-)
RispondiEliminaPiè, l'esercizietto è una mia integrazione, Paolo non è responsabile! :-)
Hai perfettamente ragione, si sarebbe dovuto precisare. Io ho (sotto)inteso unica estrazione. Mi sono potuta permettere di sottintendere trattandosi di primo approccio al calcolo delle probabilità.
quindi posso pure lasciare com'è :-)
..che poi...sarà un argomento da trattare con la terza...molto più in là...
grazie Pie'!
Elisa, caraa!
RispondiEliminasu, vado a vedere sul tuo blog! :-)
apro explorer ..che mi assista!
baci!
OT:
RispondiElimina...oggi i blog celebrano la bellezza di comunicare, e lo fanno offrendo ai propri lettori una "rosa" di altri 5 blog che amano e che vorrebbero far amare anche agli altri...
(vedi qui)
E settembre è arrivato! Buon inizio anno scolastico, Giovanna,quest'anno, insieme,sarà tutta un'altra cosa!
RispondiEliminaCiao Pier Luigi e Giovanna. Mi permetto di dissentire: se non vado errato, l'urna da scegliere dovrebbe essere la A perché contiene 6 bianche e 6 nere, infatti la probabilità di una nera è pari a 6/12 cioé al 50%. Mentre l'urna B contiene 12 bianche e 11 nere, di conseguenza la probabilità di estrarre una nera è inferiore; infatti 11/23=0,4783 cioè 47,83%. La scelta dell'urna è subordinata non tanto dal numero complessivo di palline contenute, bensì dal rapporto che vi è fra di loro. Fra l'urna A ed una C contenente 1000 palline bianche e 1000 nere la scelta sarebbe indifferente. Mentre non lo è nel caso esemplificato nell'articolo.
RispondiEliminaCol piacere di leggervi, vi saluto caldamente.
Ciao Paolo
Cia Giò, riguardo alle integrazioni nell'articolo... complimenti! Hai la didattica nel sangue! E' un piacere lavorare con te.
RispondiEliminaCiao Paolo
Ecco! S'è ricominciato dunque.
RispondiEliminaChe sia un bell'anno, Giovanna.
Un saluto caro
@pokankuni: come ho già scritto sul tuo blog: questa tua citazione mi da una carica.... :-) La ritengo perfino di buon auspicio per l'a.s. che si apre!
RispondiEliminagrazie ancora carissima e bravissima collega!
@Stella: grazie! e, è vero, insieme sarà ... meglio!:-) condividere con te mi sarà prezioso!
@Paolo: ho fatto anch'io le tue medesime considerazioni, ma devo ammettere che le precisazioni di Pier Luigi non sono errate. Se si compara probabilità e frequenza relativa di un evento, il suo ragionamento è corretto!
Ma, come ho motivato, questi sono i primi elementi del calcolo delle probabilità, dunque....
grazie per ciò che dici, grazie per il tuo contributo! E' un piacere lavorare con te! :-)
@Renata: grazie! ti rinnovo l'augurio di un buon a.s. e un caro abbraccio.
Bene, bene. Leggo con piacere che u giornalista di provincia fa discutere.
RispondiEliminaCaro Paolo gli esperimenti probabilistici hanno in comune l' incertezza del risultato, la ripetibilita' dell' esperimento, la equiprobabilita' dei risultati.
In una prova come quella che ci ha prospettato G l' incertezza del risultato deriva dal fatto che l' esperimento non e' ripetibile e anche se fosse ripetibile bisognerebb e conoscere se la pallina viene reintrotta o no. Considerato che la prova e' casuale, cioe' affidata al caso, ad un' unica prova e' indifferente la scelta dell' urna. La mano, sia nell' urna A sia nell' urna B, coniderato che le palline sono identiche, nella grandezza, nel peso, nel materiale, rugosita' e temperatura, la probabilita' che si peschi la nera e' sempre 1/2, cosi' quando si tira una moneta in aria e si gioca una volta sul testa o croce.
Tu induttivamente ritieni che anche in una sola prova sia giusto affermare che il maggior numero di palline nere possa favorire al primo colpo di vincere il premio. Nella critica alla logica induttiva il filosofo Karl Popper, epistemologo della scienza, sostiene che, perche' una teoria stia in piedi , devono esserci alcune circostanze che la dimostrino falsa.
Mi spiego con un esempio:
Io e te stiamo facendo colazione. Mentre sei intento a imburrare una fetta biscottata dici :''Non hai mai notato che se lasci cadere una fetta biscottata finisce sempre per terra dal lato imburrato?''.
Rispondo: ''No, scommetto che sembra cosi' solo perche' e' una seccatura pulire per terra quando la fetta cade dalla parte del burro. Scommetto che le probabilita' sono le stesse''.
''Ah si'? Guarda un pò''. Allora lasci cadere la fetta e questa finisce sul pavimento con la parte imburratta verso l' alto.
''Visto? Te l' avevo detto'' faccio.
Tu allora esclami: ''Oh, so io cosa ed' successo. L' ho imburrata dalla parte sbagliata''.
In pratica, scusa la celia, che pero' ha fondamenti scientifico-filosofici corretti, nessuna prova sara' mai sufficiente a falsificare la tua teoria.
Sono sicuro che i successivi post di G chiariranno bene i concetti legati al calcolo delle probabilita'.
Vale
Ahaha Pieeer,
RispondiEliminagustosissimo intervento!
Tiri fuori le leggi di Murphy!
"Se qualcosa può andare storto
lo farà"
C'è l'ironia e il paradosso no, nelle leggi di Murphy?
Che dirti? Nel semplice calcolo delle probabilità di un evento, secondo la teoria classica, dunque non frequentista: P(E)=m/n
io sarei propensa a dare la stessa risposta di Paolo.
E' vero però che uno dei punti deboli della concezione classica è la caratteristica proprietà che tutti i casi in cui può manifestarsi il fenomeno siano "egualmente possibili".
Criticata quindi, subentra in seguito il principio *dell'indifferenza* di cui tu dici....
grazie PierLui'!
G quello che dici e' giusto. Considera pero' il seguente ragionamento:
RispondiEliminai possibili risultati della prova ''estrazione di una pallina da un urna'', con palline uguali in tutto per tutto nelle loro caratteristiche fisiche, sono due: N=nera B=bianca, e solo uno tra i possibili fornisce il risultato ''si e' verificato nera'' per cui, in coerenza con la definizione classica - se i due possibili risultati sono ugualmente possibili, considerata l' unica estrazione non ripetibile - la probabilita' che esca N e'
Pr(N)=1/2.
Non si deve inoltre dimenticare che non e' possibile definire analiticamente il limite implicito nella definizione frequentista. Tale limite non e' paragonabile all' analogo concetto matematico perche' si tratta solo di una constazione empirica a posteriori dopo un gran numero di prove.
Noi filosofi parleremmo di fallacia ''post ergo propter hoc''.Si tratta dell' errore di presumere che poiche' una cosa dipende da un' altra, quella cosa e' stata causata dalla precedente. Siccome in un' urna c' e' una pallina nera in piu' si pensa che necessariamente le probalita' di estrarre alla prima prova una pallina nera e' maggiore.
Questa logica errata ci porta per esempio a dire:''la maggior parte di chi usa l' eroina ha cominciato con la marijuana''. Vero, ma sono ancora di piu' quelle che hanno cominciato con il latte.
Talora e' il propter che ci frega tute le volte, perche' non ci accorgiamo che c' e' al lavoro un' altra causa.
Si dice che i leoni non attacchino chi porta con se' una torcia elettrica.
Ti chiedo quante probabilita' ci sono che questa affermazione sia vera?
Potrei rispondere in un successivo commento, ma con la mia sorellina sono magnanimo, rispondo subito:
le probabilita' dipendono da quanto in fretta porti in giro la torcia elettrica.
La torcia, infatti, non e' una causa, ma solo un accessorio.
Vale
Cia Pier Luigi, ciao Gio. Mi rendo conto che le considerazione di Pier Luigi hanno un fondamento, però ritengo che sia più filosofico che basato sulla teoria della probabilità.
RispondiEliminaVediamo: se è vero, come credo sia vero, che la probabilità di un evento è data dal rapporto fra i casi favorevoli ed i casi egualmente possibili, non è inesatto affermare che, nel caso in esame, la probabilità di estrarre una pallina nera è più elevata sulla seconda urna.
Ma, volendo anche affrontare il problema dal punto di vista di Pier (permetti la confidenza?) mi chiedo: se nella seconda urna anziché esserci 11 su 23 palline bianche ce ne fossero 1 su 23, si potrebbe ancora affermare che la fetta di pane possa cadere dalla parte non imburrata? :))
La probabilità del verificarsi di un evento è maggiore anche quando la differenza fra le due probabilità analizzate differisce solo di qualche millesimo. Ovviamente il mio ragionamento parte dall'assunto che dell'esempio di Giovanna: una sola estrazione, due urne, la prima con 6 palline bianche e 6 palline nere, la seconda 11 palline bianche e 12 palline nere.
Scusa Pier vorrei farti una domanda provocatoria (ne va della tua vita) :):
se tu avessi di fronte due urne, la prima come già specificato, la seconda con una pallina bianca e 12 nere, se la tua vita fosse legata all'estrazione di una pallina nera, quale urna sceglieresti, quella filosofica o la B?
E se nell'urna B il rapporto bianca/nera fosse di 1 a 1.000? No, sono cattivo, 1:1.000.000.000?
Ciao Paolo
ooh, bella bella questa discussione! Mi piace!
RispondiEliminaDomani vedrò di fare le mie considerazioni... scusatemi, ho un altro lavoro ..in corso! :-)
grazie Pier Luigi e grazie Paolo.
Caro Paolo hai ragione, ma hai cambiato le regole, non piu' quelle prospettate da G. Credimi pero' che con una sola estrazione la soluzione e' sempre quella prospettata da me.
RispondiEliminaIl mio puo' sembrare un ragionamento filosofico, ma non lo e', fa perno su studi di Ramsey, Savage e Finetti, e sulla definizione classica di probabilita', utilizzata di fatto da Galilei, Pascal, Fermat, Cardano e soprattutto Laplace.
Se fosse in gioco la mia vita e le condizioni fossero quelle indicate da G credimi sarebbe indifferente la scelta dell' urna, avrei sempre il 50 per cento di scapotarla e il 50 per cento per opere di bene e non fiori.
Quando parlo da filosofo e' perche' la filosofia con la sua logica si avvicina molto alla matematica.
Prova a considerare il problema tenendo presente le leggi di de Morgan.
Ammettiamo che si estragga (una sola volta) una pallina dall' urna A (sei N e sei B)
Definiamo gli eventi
N o B= non avverra' che, contemporaneamente, sia N o B
che coincide con l' evento che avverra' che o e' N o e' B.
Stesso ragionamento vale per l' urna B (11 B e 12 N).
Le leggi di De Morgan confermano che sono solo due le operazioni essenziali dell' algebra degli eventi, cioe' o B o N, con una sola estrazione.
Anche se vi e' isomorfismo tra teoria degli insiemi e algebra degli eventi va sottolineato che gli eventi non coincidono con gli insiemi. Quindi, non si deve utilizzare la terminologia della teoria degli insiemi per il calcolo delle probabilita'.
Queste non sono considerazioni filosofiche (nota che non mi sono sentito sminuito dalla tua affermazione) ma ragionamenti basati proprio sulle teorie del calcolo delle probabilita'. Ripeto: considerati i termini proposti da G. Se tu cambi le condizioni della prova naturalmente cambiano le probabilita' che l' evento si verifichi.
Non ritengo di essere nel giusto (qui si' potrei fare una dissertazione filosofica su cosa e' giusto e su cosa non e' giusto, ma alle 2:04, il mio vecchio e stanco corpo richiede il riposo, posso avere compreso male le teorie del calcolo delle probabilita', non si deve dimenticare pero' la regola dell' incertezza del risultato nelle situazioni in cui sono possibili piu' esiti, cioe' il nostro caso.
Paolo e G un cumulativo Vale
Un abbraccio sorellina
Dimenticavo, sul discorso frequenza/probabilità, in merito al quale mi permetto di non concordare con Pier, tornerò col successivo articolo per esprimere meglio il mio pensiero.
RispondiEliminaCiao Paolo
Ah, Pier Lui'... eccomi.
RispondiEliminaNon nego che i tuoi ragionamenti spingano a delle riflessioni...
Tuttavia gli stessi (tuoi ragionamenti) mi pare vadano in ultima analisi a negare la
la definizione, data da Laplace, di probabilità secondo la concezione classica:
La probabilità P (E) di un evento E è il *rapporto* fra il numero m dei casi favorevoli (al verificarsi di E) e il numero n dei casi possibili, giudicati egualmente possibili.
Come già ho accennato sicuramente tale definizione ha i limiti, per i quali giusto si sta discutendo...:
"Inoltre il campo di applicazione della probabilità definita nel modo classico risulta molto ristretto perché la definizione *è valida* per eventi nei quali vi siano ragioni di simmetria che permettano di giudicare egualmente possibili i vari casi (come nel lancio di una moneta o di un dado non truccati, nell’estrazione dei numeri del lotto e, in generale nei problemi riconducibili a estrazione a sorte di palline da un'urna)."
Ma:
"Se non vi sono ragioni per ammettere che un caso sia più favorito di un altro, si accetta l’impostazione classica che *è utile per quei problemi che ammettono come modello matematico un'urna contenente palline eguali per forma e peso, ma distinguibili per il colore*. Tipico esempio di applicazione della concezione classica di probabilità si ha in genetica con le leggi ottenute da Mendel (verificate statisticamente da Mendel e da altri biologi ) nello studio dei problemi legati all'ereditarietà."
(da http://dida.fauser.edu/calcolo/calcol3/calcolop.htm)
Ribadisco inoltre Pier Luigi, che in questa sede (intendendo i post del blog rivolti a ragazzi della sc. media al loro primo approccio al calcolo delle probabilità), l'obiettivo è quello di introdurre gradualmente i passaggi dal vero al falso, dal certo all'impossibile... , che non sono netti ma caratterizzati da un'infinita gradazione della possibilità degli eventi:
impossibile<--->difficile<--->non certo<--->abbastanza certo<--->...<--->certo.
E per far meglio comprendere tale gradazione, mi pare opportuno creare situazioni del tipo esemplificato.
Nell'ultimo intervento, Pier, citi le leggi di De Morgan.
Ma quelle riguardano la Logica, no? L'algebra booleana. Quella per intenderci , del VERO-FALSO.
Qui siamo assolutamente nel campo della matematica-non matematica!:-) Nel senso che siamo nel pieno dell'incertezza.
Quindi, mi pare, ancora più lontani dalla Logica. Sei d'accordo fratellone?
un abbraccio
ringraziandoti sempre ...per esserci!:-)
g
Sorellina sono d' accordo. Le mie dissertazioni erano solo una risposta alle argomentazioni di Paolo e una risposta (il mio primo commento) al tuo quesito, cioe' due esperti. Ti chiedo di fare una prova pratica e vedrai che quello che dico e' reale.
RispondiEliminaAccettando per vera l' argomentazione di Paolo vedrai che l' evento N (unica estrazione) dall' urna B (11 B e 12 N) avra' due soluzioni: alla prima estrazione potra' succedere che la pallina estratta sia o N o B, cioe' avrai il 50% di probalita' che l' evento si verifichi. Ugualmente accadra' se l' estrazione sara' fatta dall' urna A (sei B e sei N). La probabilita' che l' evento si verifichi sara' sempre del 50%.
Mi spiego: se tiri fuori la N hai vinto, se invece sara' B hai perso. Questo tenendo conto di un' unica estrazione e di palline che hanno le stesse caratteristiche fisiche (grandezza, rugosita', temperatura ...). Questo credo sia comprensibile anche agli studenti di scuola media.
Tutto cambia se modifichiamo le regole, come per esempio: dopo quante estrazioni avverra' l' evento, la pallina estratta sara' eliminata o sara' rimessa nell' urna...
Ma questo, per i piu' informati ed esperti, vale anche se applica l' algebra boleana.
Nella prova di un' estrazione di una pallina da un' urna che contiene 11 B e 12 N, gli eventi N=pallina estratta e' nera e B=pallina estratta e' bianca, non sono equiprobabili per cui non si puo' applicare la regola pratica per il calcolo delle probabilita' di N e B.
Tuttavia se si considerano le singole 11+12=23 palline, le quali a prescindere dal colore hanno tutte la stessa forma, peso, rugosita' ... allora l' estrazione di ciascuna delle 23 palline genera una serie di eventi che costituiscono una partizione equiprobabile della prova: infatti non si vede perche' una delle 23 palline debba avere una probabilita' diversa dalle altre essendo le 23 palline indistinguibili tra loro.
Grazie G e grazie P per avermi aiutato a ricordare concetti che spesso sono lontani, ma non troppo, dalla mentalita' umanista.
Un abbraccio dal fratellone.
Un cumulativo Vale
ook, Pie'! :-)
RispondiEliminagrazie e un abbraccione!
Ciao Gio, ciao Pier. Prima una precisazione: Pier, hai interpretato correttamente il fatto che non volevo essere offensivo quando ho parlato di concezione filosofica, anzi tutto il mio rispetto per tale scienza.
RispondiEliminaMa, brevemente, una domanda:
se, ammettendo per un momento (sia chiaro solo per un momento :-)) che da un'urna con 11 bianche e 12 nere una sola estrazione può generare una bianca o una nera al 50% (in base al ragionamento che la pallina è o B o N), perché lo stesso concetto non dovrebbe valere se il rapporto bianche/nere cambiasse in 1/1.000.000. Se l'assunto vale per un caso deve valere per tutti i casi come insegnano le scienze "esatte".
Non vorrei che il ragionamento alternativo,seppure culturalmente stimolante, ci portasse anche ad accettare "dimostrazioni per assurdo" quali, solo per citare, i paradossi di Zenone: Achille raggiungerà la tartaruga?
Ciao e grazie ad ambedue per la dotta (da parte vostra) discussione.
Paolo
Paolo i tuoi ragionamenti dal punto di vista del calcolo probabilistico sono corretti. Sono esatti anche applicati al test proposto da G, alla quale sicuramente gira la testa nel seguire il nostro ping e pong (o pong e ping?, va be' quella cosa li').
RispondiEliminaNon per essere innamorato della mia spiegazione ma, PRATICAMENTE, la probabilita' che esca N alla sola unica prova a disposizione e' sempre uguale al 50%. Infatti, tu metti la mano nell' urna, mescoli bene, prendi una pallina e la tiri fuori, puo' essere N o B. Ripeto in un' unica sola non ripetibile prova la probabilita' che l' evento si verifichi e' del 50%.
Conosci la fallacia di Montecarlo?
I giocatori d' azzardo la conoscono molto bene, anche se molti sono poi sorpresi di scoprire che si tratta di fallacia. La considerano anzi una strategia (la strategia Montecarlo, appunto). In realta' i croupier ci contano.
La ruota della roulette ha meta' numeri N e meta' R. Se facciamo girare la ruota un numero elevato di volte - diciamo 10000 - e la ruota non e' truccata o difettosa, la pallina dovrebbe fermarsi in media 5000 volte sul R. Cosi', se facciamo girare la ruota 500 volte e si ferma 500 volte sul N, siamo tentati di pensare che le probabilita' siano a nostro favore se al 501/mo giro puntiamo sul R.
Tocca per forza al R, giusto?
Sbagliato, invece.
La pallina ha esattamente lo stesso 50% di probabilita' di fermarsi sul R che ha avuto nelle precedenti 500 giocate, e questo varrebbe indipendentemente dal numero di volte che il N esce di seguito.
Paolo, una domanda personale, viaggi? molto? in treno? in aereo?
Bene!
Se devi prendere un treno, per sicurezza, portati una bomba ... perche' ci sono probabilita' schiaccianti che sullo stesso treno NON CI SIANO DUE TIZI con una bomba.
Grazie ''sorellina'', per la pazienza, per i tuoi illuminanti commenti, grazie Paolo per l' interessantte dibattito.
Perdonate l' intrusione di un caparbio giornalista di provincia.
Vale
Pier "fratellone",
RispondiEliminagrazie a te!
mi diverto un mondo invece..:-)
Evvaiii!
non posso trattenermi...faccio tardi a scuola!
bacioni!
Ciao Pier, ecco, hai perfettamente inquadrato il problema sul quale la teoria delle probabilità ha una posizione completamente divergente dalla tua. Il "Teorema della probabilità composta" o "delle prove ripetute" è esauriente al proposito e sarà oggetto di uno specifico articolo. ammesso che Giovanna abbia la bontà di pubblicarlo. Ma, caparbietà per caparbietà.... se a seguito di 1.000 lanci di una moneta, fosse uscito 1.000 volte "testa" e ti venisse detto: se indovini la prossima uscita ti "ricresceranno i capelli" mentre se non indovini ti "@#!?#@....", quale risultato sceglieresti? Se la tua risposta è come penso, e non potrebbe essere altrimenti, spiacente ma non ti ricresceranno mai i capelli, anzi, ti "@#!?#@....".
RispondiEliminaSi fa anche per scherzare un pò, no? D'altronde, nonostante la mia ferma convinzione, io non ho mai indovinato, infatti sono senza capelli.
Ciao Paolo
ciao Pier e ciao Paolo, tho son capitati "Pietro e Paolo" :-) :-)
RispondiEliminavi ringrazio io entrambi per l'interessante dibattito!
Ora attendo con ansia il seguito del lavoro di Paolo.
Immagino sia da inquadrare: "Frequenza relativa e probabilità"
Bene!
Il dibattito continua :-)
Me lo auguro!
grazie ancora a voi.