Le abbiamo viste in classe.
Ho riportato su Geogebra le osservazioni sulle simmetrie del quadrato, nelle quali abbiamo riconosciuto analogie di struttura: operazioni geometriche, operazioni aritmetiche, operazioni logiche... elementi e operazioni del tutto diverse dove si ripete però lo stesso motivo, la stessa struttura!
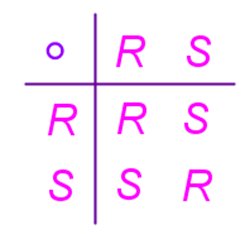
A partire da questa immagine:
osservando particolari coppie di figure, ci si accorge che alcune coppie sono inversamente uguali, ottenute perciò con un ribaltamento, altre sono direttamente uguali, si ottengono senza che la figura si sollevi dal piano, come avviene ad es. con la rotazione.
Sull’applet, potete interagire, sono riportate le composizioni di simmetrie e rotazioni e
la tabella di composizione:
Ragazzi, qui vi sottolineo un particolare sulla composizione delle due simmetrie assiali. E’ noto come il Teorema dei due ribaltamenti:
Il prodotto di due simmetrie assiali rispetto ad assi incidenti equivale alla rotazione, intorno al loro punto di intersezione, di ampiezza pari al doppio dell’angolo formato dagli assi di simmetria.
Verificatelo sull’applet.
Ricordiamo le strutture analoghe, viste l’anno scorso (clic sulle immagini, sono le vostre relazioni):
Tabella dell’addizione del Pari e Dispari
Tabella di composizione del Sì e del No
E la tavola dell'addizione dello zero e dell'uno
Attenzione! Non c'è un errore nell'ultima casella in basso: 1+1 non fa 0 nella nostra aritmetica, ma in un’aritmetica che ancora dobbiamo scoprire, quella delle "classi resto [0] modulo 2", sì! (per il momento stabiliamo soltanto che i simboli 0 e 1 stanno ad indicare, in modo breve, i termini pari e dispari: i numeri pari sono i numeri che divisi per 2 danno resto 0 e i numeri dispari sono i numeri che divisi per 2 danno resto 1)
Potete scaricare un file Excel tab_Pari_Dispari.xls dove troverete, anche la legge moltiplicativa oltre a quella additiva.


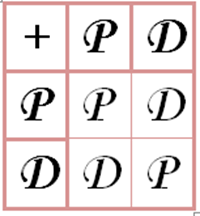
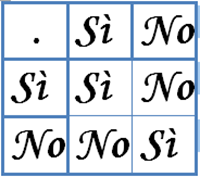

























Nessun commento:
Posta un commento
I vostri commenti sono graditissimi, l'interazione è molto utile!
Non ci piace però comunicare con "anonimi". Vi preghiamo di firmare i vostri messaggi.
Come fare:
Cliccare su Nome/URL.
Inserire il vostro nickname nel campo "nome".
Lasciate vuoto il campo URL se non avete un blog/sito.
Grazie!