Il triangolo di Reuleaux

Il triangolo di Reuleaux,
dal nome dell’ingegnere e matematico tedesco Franz Reuleaux (1829-1905) è la più semplice delle curve ad ampiezza costante. La più semplice dopo la circonferenza. La più nota di tali curve infatti è la circonferenza.
E cioè:
un cerchio che rotola su una retta rimane sempre nella porzione di piano compresa tra la retta e
la sua parallela, a distanza uguale al diametro del cerchio.

Nel muoversi il cerchio è sempre in contatto con entrambe le rette: è una figura di ampiezza costante.
Si possono costruire altre figure con la stessa proprietà!
Il triangolo di Reuleaux.

Si costruisce partendo da un triangolo equilatero;
si tracciano tre archi di cerchio:
- centro su A, raggio uguale al lato del triangolo, estremi i vertici B e C
- centro su B, raggio come sopra, estremi A e C
- centro su C, raggio ..., estremi A e B
Osserviamo: l’ampiezza di questa figura è uguale alla lunghezza del lato del triangolo equilatero.
Figure più generali dei triangoli di Reauleaux sono i poligoni di Reuleaux; si costruiscono utilizzando un qualsiasi poligono regolare convesso con un numero dispari di lati. Es:

Queste figure sono costituite da un numero dispari di archi di cerchio di ugual raggio (in questo caso la lunghezza delle diagonali del poligono) e possiedono lo stesso numero di vertici, i punti di raccordo tra due archi di cerchio consecutivi.
"Per ottenere figure di ampiezza costanti non è necessario considerare esclusivamente poligoni regolari con un numero dispari di vertici; si può anche utilizzare un poligono irregolare convesso per il quale le lunghezze delle diagonali del poligono che congiungono ciascun vertice coi due vertici opposti sono tutte uguali tra loro. In tal modo dal poligono di partenza si possono tracciare i vari archi di cerchio con raggio uguale alla suddetta diagonale."
clic sull'immagine per ampliamenti...

Ma torniamo al *triangolo* di Reuleaux.
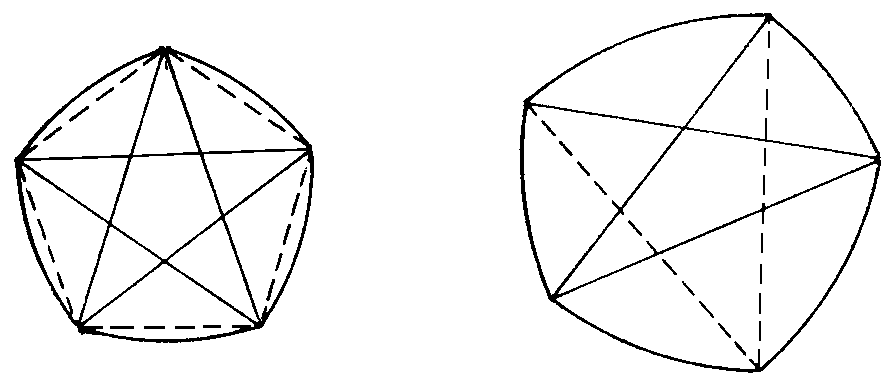
Clic sull'immagine per osservarlo in movimento e verificarne l'ampiezza costante.

Potrete agire sul punto rosso zieh' mich! (trascinami) per far scorrere il triangolo. Uno slider permette di variare l'ampiezza della figura e infine, agendo ancora su un altro slider, si può osservare la traccia del centro del triangolo.
Il triangolo di Reuleaux può ruotare in un quadrato, appoggiandosi sui lati con i suoi vertici.
Clic per vedere l'animazione (da geogebra wiki en):

Infine, il triangolo di Reuleaux di Daniel Mentrard

E:
Le tétraèdre de Reuleaux,
Perimetro e area
Interessante anche questa pagina.

Articoli correlati per categorie