“Le gaie colpiscono ancora!”
Così mi scrivono nell’oggetto della loro mail, Letizia, Maria Chiara ...+ Erica e naturalmente Silvia la secchiona (io copio-incollo, Silvia non esiste da noi in terza, è un loro gioco – chissà cosa vogliono non ammettere ... ?)
Insomma, mi inviano la cronaca della lezione di ieri.
Un nuovo inizio … e ripasso.
Eccola giunta alla nostra classe, la prof Arcadu, tutta pimpante ed euforica, nella sua mente il progetto sullo svolgimento della lezione.
Infatti non vedeva l’ora di presentare il nuovo argomento di matematica.
Ci dice: "Oggi si comincia a operare con i numeri relativi!" E poi:
“Ricordate vero? L'insieme dei numeri relativi, perché si chiamano relativi?" [mai l'avesse fatto, NdP, nota della prof!]
Noi ricordavamo i numeri relativi, introdotti con le sottrazioni non fattibili in N: quelli con il segno + e –. Però: perché si chiamano relativi??? Tutti zitti!
La prof ci ha detto: "oggi fuori ci sono 10 gradi di temperatura", e ci ha chiesto se avessimo qualcosa da contestare, così noi le abbiamo chiesto [non così immediatamente, NdP]: "- 10° o +10° gradi? ".
La sua risposta è stata "oh cari ragazzi è proprio quello che volevo sentirvi dire, allora il valore del numero dipende dal segno che lo precede, è relativo al segno!"
In seguito abbiamo ricordato i vari insiemi recitando [leggendo insieme, allegra … confusione, ahimè! NdP] alcune poesie citate dalla prof durante l’estate facendo riferimento al Prof. Popinga:
L'insieme N: quello dei numeri naturali, è sottoinsieme di Q
L’insieme N
Numeri naturali son quegli enti
che contiamo sulle dita,
senza di lor la nostra vita
sarebbe assi più complicat.
Sol più tardi è stato aggiunto
quel pallin che è lo zero:
per gli antichi era mistero
una cifra valente nient.
Insieme Q: dei numeri razionali (abbiamo anche detto che il numero razionale è un intera classe di equivalenza ovvero un insieme di frazioni equivalenti a una data primitiva, è un quoziente fra due interi, incontrato nelle divisioni non fattibili in N)
L’insieme Q
E’ l’insiem dei razionali,
con la virgola o le frazioni:
corrispondon alle divisioni
tra numeratore e denominator.
Diversamente dai naturali,
non si contan sulle dita:
si rischierebbe persin la vita
a far frazioni delle falang.
Insieme I: dei numeri irrazionali ovvero le radici di numeri non quadrati perfetti e i quozienti fra 2 grandezze incommensurabili (quelle che non hanno sottomultipli in comune, nemmeno l’1) es, Pi greco…
Insieme R (dei numeri reali, quelli che esistono, perché ci sono anche i numeri immaginari!): esso è dato da Q ∪ I=R, include tutti gli insiemi precedentemente elencati. Ma l'insieme Q include l'insieme Z, nel quale abbiamo operato oggi.
Siamo stati in grado di dire, dopo l‘esempio iniziale della prof, che l’insieme Z è l’insieme dei numeri interi relativi quindi Z = Z+ ∪ Z- ovvero l’unione dei numeri interi relativi, positivi e negativi.
L’insieme Z
E’ l’insiem dei relativi
che sono numeri con il segno:
una trovata di vero ingegno;
senza segno è ‘l valore assolut.
Sol con essi si può fare
ogni tipo di sottrazione:
era proprio contraddizione
togliere sette da cinque dit.
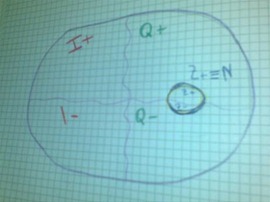
Ecco la rappresentazione dei numeri Reali con il diagramma di Eulero Venn:
Insieme dei numeri Reali relativi include I+ e Q+ , I- e Q- L’insieme Z+ è sottoinsieme di Q+ e Z- di Q- , Z+ coincide con N.
La prof ha pensato poi di farci ripassare la
Rappresentazione dei numeri Reali sulla retta
Ha fatto disegnare a tutti sul quaderno una semiretta nella quale abbiamo inserito i numeri naturali ricordandoci che ad ogni numero naturale corrisponde un punto della semiretta ma non è altrettanto vero il contrario, dire che ad ogni punto della semiretta corrisponde un numero naturale.
Per poter avere anche i numeri negativi dovevamo far diventare quella semiretta una retta.
Ora dovevamo riempire di numeri i punti tra due numeri naturali. Abbiamo inserito i numeri razionali, per esempio 3/2:
l'unità, da zero a 1, la dividiamo in 2 parti e ne prendiamo 3, per quanto questa possa essere una spiegazione infantile e banale considerate le nostre conoscenze, ci è stata molto d’aiuto!
Uff… !!!!!!!!!!: neanche con i numeri razionali siamo riusciti a occupare tutti i punti della retta. Cosi abbiamo collocato i numeri irrazionali rispolverando così i lavori precedentemente pubblicati sul blog come il lavoro di Gabriele che ci è stato utile per inserire le radici quadrate:
E, I numeri Reali assoluti sulla semiretta numerica
Naturalmente a sinistra dello zero posizionavamo i negativi, sia razionali che irrazionali. Ora con tutti i Reali, Q ∪ I, abbiamo occupato tutti i punti della retta, come ci aveva anticipato la prof quando eravamo all’inizio del nostro percorso, in prima media.
E finalmente ci siamo dedicati alle prime operazioni in Z: la prima scoperta è stata che in Z si perde un po' la distinzione delle operazioni in: addizione e sottrazione. Si tratta di "fare un bilancio": tra negativi e positivi, come tra debito e credito, soldi che ho in tasca e soldi che devo! Si parla di somme algebriche.
FINE
by, le alunne “croce e delizia”
Brave, delizie! (oh, per esservi dedicate di Sabato pomeriggio, eh eh...)
Raga, da leggere:



























Passo per un breve saluto, prima di partire per qualche giorno per L'Aquila. A presto, Fabio
RispondiElimina