Sarà mica matematica 38, le nostre soluzioni

Ed ecco le nostre soluzioni del

Sarà mica matematica n° 38

Che dire? Qualcuno batte la fiacca, qualcuno trova difficoltà, qualcuno comunque ci prova, qualcuno trova le soluzioni ma non le spiega… insomma di tutto un po’. Anche il numero di solutori è un po’!

Quesito 1, le date di nascita

Per la classe prima risolvono: Yuri, Andrea, Marta C. (per tentativi trova due date ma non la terza), Elena (che non spiega), Paola, Roberta (per tentativi), Aurora (come Marta C.), Antonio, Sara (che non spiega), Luca.

Per la terza: Antonella e Gian Franco, Alessia, Giuseppe P.

Le risposte più complete ed esaurienti sono simili a quella di Giuseppe P., che copio-incollo:

Secondo me Paolone è nato nel 1958, ho proceduto svolgendo la seguente operazione: 116:2=58. Ho considerato il 1900, ho dovuto calcolare la differenza tra 2016 e 1900= 116. Poi dividerla per due perchè l'età deve corrispondere alle ultime 2 cifre dell'anno di nascita.

Paolino ha 8 anni, ho tratto questa conclusione prendendo in considerazione gli anni 2000, 2016-2000= 16:2=8. Paolino è nato nel 2008.

Seguendo lo stesso ragionamento, la persona denominata Io [e sì, “Io” è stato da alcuni identificato con il prof Davide, altri hanno avuto qualche dubbio, chissà perché… Mah, io non voglio dirlo! Che abbiano fatto paragoni??Qualcuno, non volendosi sbilanciare, ha scritto anche “età di io: ha 47 anni ed è nato nel 1969” ] avrà la stessa coincidenza nel 2038, quando avrà 69 anni, essendo nato nel 1969.  2038- 1900= 138;  138: 2= 69. 

Quesito 2, i marmi dei mosaici

Per la classe prima i solutori: Andrea, Yuri, Paola, Roberta, Aurora (che somma le aree utilizzando la costruzione su Geogebra), Davide (realizza la costruzione corretta su Geogebra ma fa dei ragionamenti complicatissimi e non riporta il risultato finale corretto), Antonio, Marta C., Roberta, Sara, Luca.

Per la terza: Antonella e Gian Franco, Alessia, Giuseppe P., Elisa, Miriam.

Cominciamo con una delle costruzioni realizzate con Geogebra, questa è di Roberta:

Dato il perimetro del quadrato complessivo, di 16 cm, si chiedeva l'area della superfice in marmo bianco.

Roberta, come altri, spiega così:

 L’area del marmo bianco è di 12 cm².

Faccio innanzitutto 16/4=4 cm e ottengo la misura di un lato del quadrato grande.
Poi: 4/2=2 cm e ottengo la misura di un lato del quadrato medio.
Quindi: 2*2=4 cm² e ottengo l'area di un quadrato medio bianco.
Moltiplico per 2 perché i quadrati medi sono due: 4cm²*2=8 cm² e ottengo l'area dei quadrati medi bianchi.
A questo punto ho osservato attentamente la figura e con le parti rosse, dei triangoli, ho formato due figure identiche corrispondenti al quadrato piccolo bianco:

Questo significa che un quadrato piccolo bianco corrisponde alla metà di un quadrato medio.
Quindi ho fatto 4cm²/2=2 cm² e ottengo l'area di un quadrato bianco piccolo, ma i quadrati piccoli sono 2 quindi 2cm²*2=4 cm² [E tanto valeva…!]
Infine ho fatto 8 cm²+4 cm²=12 cm²

Di Paola mi è piaciuta la spiegazione del perché i quadrati piccoli sono equivalenti alla metà dei medi:

Perché se ruoto di 180 gradi un triangolo di marmo rosso combacia perfettamente con 1/4 di un quadrato minore di marmo bianco. [li ha ruotati tutti e quattro e colorato in bianco i triangoli corrispondenti nelle rotazioni]

I punti con etichetta sono i centri di rotazione.

Altri:

dividono il quadrato medio in 8 triangoli rettangoli uguali e ne “prendono” la metà, ovvero 4, che quindi equivalgono alla metà del quadrato medio.

Altri ancora:

considero il lato di un triangolino=1 cm; area di un triangolino: 0.5 cmq; 0,5*4=2 cmq=area di 4 triangolini= area di uno dei quadrati piccoli.

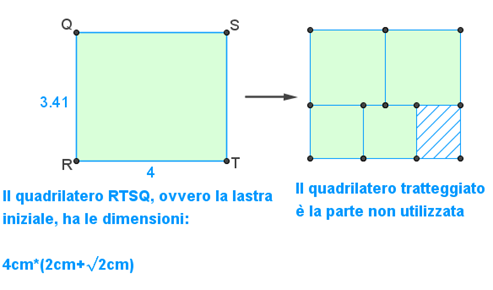
Infine, la domanda aggiuntiva per secondini e terzini: quali le dimensioni minime della lastra bianca iniziale intera da cui sono stati ricavati i pezzi bianchi?

La risposta è stata data solamente da Alessia e dai cuginetti Lella (che sarebbe Antonella) e Gianfri (che sarebbe Gian Franco)

Alessia invia la costruzione:

Lascia intuire a me che ha trovato il lato dei quadrati piccoli pari a √2 cm.

I cuginetti dicono:

Se il lato dei triangolini rossi che sono rettangoli isosceli, è di 1 cm, secondo il teorema di Pitagora il lato del quadrato piccolo è uguale a √2 cm quindi:

la lastra bianca iniziale è formata dai 4 quadrati bianchi di dimensioni 2 cm e √2 cm che uniti formano un rettangolo (aggiungendo il pezzo tratteggiato) delle seguenti dimensioni:

E bravi Alessia e cuginetti! – Visto che sono stati gli unici.

Quesito 3 le spirali nei mosaici

Il prof Davide ha ricostruito un particolare su Geogebra

E la domanda: Se il lato del quadrato misura 10 cm, qual è la lunghezza complessiva delle linee nere della spirale?

Per la classe prima risolvono: Paola, Roberta, Yuri, Aurora (spiega ma non riporta la lunghezza totale della spirale), Antonio, Elena, Sara, Andrea, Luca.

Per la terza: Antonella e Gian Franco, Arianna, Alessia, Giuseppe P., Miriam.

Diverse le risposte del tipo:

La lunghezza complessiva delle 2 linee nere della spirale è di 60 cm. Ogni linea nera è composta da 2 parti che misurano 7.5 cm ciascuna e altre 3 parti da 5 cm. La lunghezza di una delle linee nere della spirale è di 30 cm: (7.5x2) + (3x5)= 30 cm. 30x2= 60 cm.

Qualcuno scrive:

la spirale comprende:
i 3/4 di ogni lato cioè 3/4 di 10 cm=7.5 cm, che si ripetono sui 4 lati, quindi: 7.5×4 =30 cm;
attraversa l’interno del quadrato con 1/2 del lato per 6 volte, cioè 5×6=30 cm.
La lunghezza complessiva della spirale è perciò di 60 cm.

Più originale la soluzione di Antonio (non precisissime le costruzioni):

trasforma la spirale iniziale

in questa:

Trasporto le due linee che passano al centro del quadrato, tagliate a metà, sui lati del quadrato per averli interi, quindi ho 4 lati da 10 cm: 10x4 = 40 cm. Rimangono 4 linee all’interno da 5 cm ciascuna: 5x4 = 20 cm. La lunghezza totale è: 40 cm + 20 cm = 60 cm.

Ho concluso, se scordo qualcuno mi si faccia notare.

Grazie come sempre al prof Davide,

Bravo a chi ha lavorato e anche a chi ci ha provato.

Oh, i nuovi quesiti spettano a me!

Qualcosa è già pronto, pubblicherò appena completo. A prestissimo!

Articoli correlati per categorie