Ecco le nostre soluzioni del bellissimo
Sarà mica matematica 33 del prof Davide.
La Piazza Grande di Palmanova ci ha dato una bella occasione, in seconda, per scoprire le proprietà dell’esagono regolare che ancora non avevamo visto.
I solutori del quesito si sono dati da fare per lavorare sull’esagono ed essere poi in grado di rispondere correttamente. Hanno fatto molto da soli, lodi lodi, anche se non è mancato un piccolo aiuto da parte della nostra insegnante di sostegno... che me li coccola! Ma sì, ma sì, bene...
La spiegazione completa non è arrivata proprio da tutti ma va bene così. Per stavolta!
Bene, andiamo alle soluzioni e ai solutori.
Quesito 1, la Piazza appunto
Per la classe seconda risolvono: Alessia, Elisa, Gianfranco, Antonella, Giuseppe P., Arianna
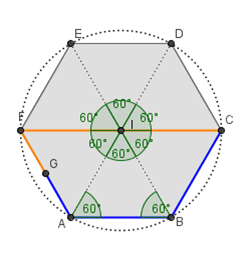
Tutti arrivano alla corretta soluzione mediante questa figura (la costruzione è di Gian Franco, ho nascosto per ora un elemento...):
Affermano, sintetizzo le risposte, che:
le diagonali dell'esagono, che sono tre, si incontrano in uno stesso punto che è equidistante dai vertici. Le tre diagonali dividono l'esagono in 6 triangoli equilateri. Quindi i due percorsi sono uguali perché: quello arancione è formato da due lati (uno di un triangolo, uno di un altro triangolo) più metà di un altro lato, il percorso blu è formato da due lati dell'esagono (che sono anche le basi di due triangoli) più metà di un altro lato. Essendo i triangoli tutti equilateri, di conseguenza i due percorsi sono uguali.
Sì, va bene, ma la prof ha chiesto anche di dimostrare perché quei triangoli sono equilateri. Come facciamo ad esserne sicuri?
Le risposte complete sono arrivate da Gian Franco e Alessia. Alessia scrive per la dimostrazione:
l'esagono è diviso in 6 triangoli equilateri-equiangoli perché: l'angolo centrale di 360° è diviso in 6 parti dalle diagonali che si incontrano [nel centro della circonferenza circoscritta]. Ogni angolo misura 60°.
Siccome i triangoli sono isosceli perché due lati sono raggi della circonferenza circoscritta, i due angoli alla base sono congruenti e misurano ciascuno: (180° - 60°) : 2= 60°. Quindi i triangoli sono equiangoli e perciò equilateri.
Noto ora che Alessietta non ha inviato immagini, sfruttiamo quella di GianFranco (mostro ora la circonferenza circoscritta):
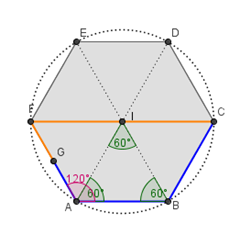
Gian Franco scrive:
Gli angoli interni dell’esagono regolare sono di 120°. Se dell'esagono traccio le diagonali (che equivalgono alle bisettrici) divido il poligono in 6 triangoli uguali, formati da due raggi della circonferenza circoscritta e un lato dell'esagono. I triangoli sono equilateri. Però di questo non sono sicuro allora devo dimostrarlo. Quindi ho pensato che siccome le bisettrici dividono l'angolo a metà, due angoli di ogni triangolo sono congruenti e misurano ciascuno 60° [sono gli angoli alla base del triangolo isoscele: due lati sono congruenti perché raggi della circonferenza circoscritta]. Qui ho pensato a come poteva essere l'altro angolo e siccome la somma degli angoli di tutti i triangoli del mondo è di 180° [], togliendo da questo i due 60° ottenevo nuovamente 60°. Questo significa che il triangolo è equiangolo e quindi anche equilatero.
La figura che mostra la spiegazione di Gian Franco dovrebbe essere questa:
Bene. Ora i solutori della classe terza: Manuel, Bachisio, Pierluigi, Gabriele G., Pietro P.
La spiegazione completa, con dimostrazione riguardante i triangoli equilateri, è fornita solo da Bachisio e Pietro.
La dimostrazione è simile a quella di Alessia, Pietro lavora solo sull’angolo al centro di 180° (la costruzione originale è di Manuel, ho aggiunto l’angolo al centro e la circonferenza): i percorsi sono uguali perché abbiamo dei triangoli equilateri. Però resta da stabilire perché sono equilateri: perché se tracciassimo la circonferenza circoscritta all'esagono vedremo che due lati sono uguali, quindi abbiamo dei triangoli isosceli, poi dividiamo l'angolo al centro in tre angoli uguali. Avendo anche gli altri due uguali capisco che sono equilateri. [più sintetici di così....]
Passiamo al Quesito 2, coltivazioni e matematica, dice Alessia
Risolvono per la seconda: Alessia, Elisa, Gianfranco, Antonella, Giuseppe P., Arianna, Miriam.
Il prof Davide ha piantato 9 zucchine, 18 melanzane, 36 pomodori, 54 fagioli.
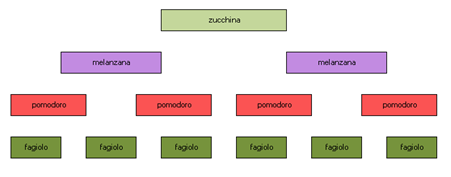
Spiegano bene tutti e si sono aiutati con uno schemino tipo questo:
Lo schema è di Miriam e copio incollo la sua spiegazione, bella chiara, ci dice passo a passo...
Ho lavorato aiutandomi con degli stuzzicadenti, seguendo passo passo ciò che mi diceva il problema.
Esso diceva che "Per ogni seme di zucchina ne ho piantati due di melanzane". Perciò ho posizionato sul tavolo uno stuzzicadenti rappresentante il seme della zucchina e sotto due stuzzicadenti che rappresentavano i semi delle melanzane.
Fino a quel momento avevo 3 semi.
Poi il problema mi diceva che "Per ogni seme di melanzana ne piantati due di pomodoro", quindi, sotto ogni seme di melanzana ho posizionato 2 stuzzicadenti che rappresentavano i due semi di pomodoro.
Quindi avevo 7 semi.
Ho continuato a leggere il problema, l'ultimo dato che mi forniva il problema era che "Per decidere quanti fagioli seminare ho contato i semi di melanzane e pomodori, sommati, e ne ho piantati altrettanti di fagioli", quindi, siccome i semi di melanzane e pomodori sommati sono 6 (2 melanzane + 4 pomodori) ho piantato 6 semi di fagioli, 3 sotto i due di pomodori, e i 3 restanti sotto gli altri 2 di pomodori.
Avevo 13 semi.
Sapevo che per trovare quei tredici semi ero partita da un solo seme di zucchina, però in totale c'erano 117 semi.
Per sapere quante volte si erano "ripetuti" quei 13 semi ho fatto 117 : 13 = 9
Poi ho moltiplicato per 9 i semi di partenza delle diverse varietà, quindi:
1 seme di zucchina x 9 = 9 semi di zucchine
2 semi di melanzane x 9 = 18 semi di melanzane
4 semi di pomodori x 9 = 36 semi di pomodoro
6 semi di fagiolo x 9 = 54 semi di fagiolo
infatti, 9 + 18 + 36 + 54 = 117.
Gian Franco arriva a mostrare l’orto completo del prof Davide!
Copio incollo spiegazione e immagine dal suo foglio di Excel
Per la terza rispondono: Manuel, Bachisio, Pierluigi, Gabriele G., Pietro P.
E, loro sono in terza! Sono stati bravi, devo dirlo. Non abbiamo ancora fatto le equazioni ma, ispirati dai monomi, dicono, hanno impostato, quasi tutti correttamente, un’equazione risolutiva del problema:
indico i semi di zucchina con la x, i semi di melanzana sono il doppio dei semi di zucchina quindi 2x;
i semi di pomodori sono il doppio dei semi di melanzana quindi il quadruplo di quelli di zucchina cioè 4x;
i semi di fagioli sono la somma dei semi di melanzana e pomodoro quindi 6x;
117= x + 2x + 4x + 6x
117= 13x
x= 117/13 = 9 semi di zucchina
9*2=18 (semi di melanzana)
18*2=36 (semi di pomodoro)
18+36=54 (semi di fagioli)
9+18+36+54=117
Bene, bene. Eh, dico così: ovviamente, per chi ha lavorato! Sempre pochi, ahimè. Ma sanno tutti bene che ognuno si assume le proprie responsabilità!
E mi pare di non aver scordato niente...
Grazie, come sempre, stavolta ancora di più, al prof Davide!
Domani pomeriggio dovrebbero essere qui i nuovi quesiti





























Bravi, cos'altro dire? Davvero bravi, quelli che hanno lavorato!
RispondiEliminaBelle, come sempre le costruzioni con Geogebra. Molto bello l'orto con Excel!
Pochi ma buoni, insomma :-)
Io sto per pubblicare - finalmente - le "nostre" risposte ma non sono altrettanto soddisfatto. Spero nei nuovi quesiti :-D
grazie prof.
RispondiEliminaSì sì, infatti mi godo quelli, pochi e quando sono buoni :-)
I nuovi quesiti... ho provato ad essere buonissima! Ci tocca :-)
vado a leggervi....