Arrivano le soluzioni del
Lavorano sempre più o meno le stesse persone, mi sento di lodare Daniele della classe prima, che si aggiunge ai solutori abituali.
Ovviamente c’è chi lavora con più cura e chi un po’ meno. Chi lo fa un po’ meno spero sia stimolato (e un po’ d’orgoglio no?) da chi dà il meglio!
E a dare il meglio, stavolta occorre proprio sottolinearlo, sono stati i ragazzi della prima. Si sono distinti in particolare nella soluzione del quesito geometrico, con l’utilizzo di GeoGebra, tenuto conto della loro più recente conoscenza del programma e della minore conoscenza delle proprietà geometriche dei poligoni. Proprietà che proprio attraverso Geogebra essi hanno scoperto praticamente da soli.
Veniamo alle soluzioni.
Quesito 1, numerico, nel quale si chiedeva di unire insieme quattro cifre dispari per ottenere quale loro somma il numero 21.
Per la Classe prima hanno risposto: Alessia, Giuseppe P., Daniele, Antonio, Gian Franco.
Per la seconda: Manuel, Bachisio, Pietro S., Gabriele G., Marco, Pierluigi, Pietro P. e Davide A.
Quasi tutti i solutori hanno intuito subito lo stratagemma da utilizzare per la soluzione (il primissimo è stato Giuseppe P.!)
La spiegazione più chiara e meglio espressa è stata, a mio giudizio, quella di Alessia:
Ho fatto valere un 1 x 10, cioè 1=10, messo una cifra dispari al posto delle unità e poi ho aggiunto le 2 cifre dispari che mi servivano per ottenere 21.
Le soluzioni:
11+7+3=21
11+5+5=21
13+7+1=21
13+5+3=21
15+5+1=21
15+3+3=21
17+3+1=21
Per la risposta alla domandina iniziale (secondo voi usando quattro cifre dispari possiamo ottenere una somma dispari?) ho chiesto si argomentasse generalizzando, dunque ricorrendo alle lettere al posto dei numeri.
Tutti (la seconda avvantaggiata dall’esperienza) hanno saputo esprimere un numero pari qualsiasi nella forma 2n e uno qualsiasi dispari nella forma 2n±1. Nella dimostrazione della somma di quattro numeri dispari sono stati appena più celeri sempre i ragazzi della seconda, ma più originali quelli della prima nel dimostrare la somma di quattro diversi dispari:
2n+1 + 2n-1 + 2n+3 - 2n-3 = 8n
La somma di quattro numeri dispari è un numero pari.
Quesito 2, geometrico, la scomposizione di un triangolo equilatero, estesa a tutti i poligoni regolari, in n (numero di lati del poligono) quadrilateri congruenti.
Per la classe prima, i solutori: Alessia, Miriam, Gian Franco, Daniele.
Per la seconda: Davide A., Manuel, Marco, Bachisio, Pietro S., Gabriele G. e Pietro P. (solo Manuel e Marco estendono le costruzioni a più poligoni)
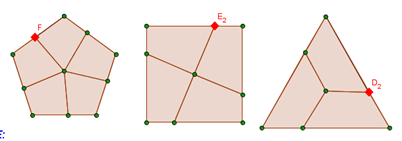
Sotto, le immagini risolutive del triangolo e del pentagono. Dalle costruzioni di Marco (II), statiche – Marco ha scomposto 6 poligoni regolari.
Non sono state fornite chiare e complete spiegazioni se non quella di aver trovato il centro dei poligoni con l’intersezione delle bisettrici degli angoli [che poi nei poligoni regolari coincidono con gli assi dei lati e con le mediane e nel triangolo equilatero anche con le altezze].
Ho parlato di costruzioni statiche. Sì, a fronte di quelle dinamiche che Geogebra permette e da me richieste o auspicate!
Fatto sta che solo Alessia, Gian Franco e Miriam della prima hanno correttamente costruito le soluzioni dinamiche.
Il lavoro di Alessia sul triangolo. - Ha costruito anche il pentagono. Clic su immagine per aprire l’applet.
Il lavoro di Miriam sul quadrato. - Costruito anche il triangolo. Clic
Il lavoro di Gian Franco. Con spiegazioni sul foglio di lavoro. Clic:
La spiegazione più carina della costruzione, direi un piccolo tutorial è quella scritta da Alessia. Può essere utile, eccola:
Prima costruisci il triangolo equilatero senza usare lo strumento di geogebra, Poligono regolare. Come fare :
- tracci un segmento a piacere: A - B
- prendi lo strumento Circonferenza dati centro e un punto
- usa, come centro della circonferenza, il punto A e, come punto (della circonferenza) il punto B
- rifai la stessa cosa ma al contrario, cioè il punto B diventerà il centro della circonferenza e il punto A diventerà il punto della circonferenza
- intersechi le due circonferenze (strumento Intersezione di due oggetti) e costruisci il triangolo
- infine nascondi le circonferenze
Triangolo equilatero scomposto, "dinamico". Come fare :
- cerchi il centro del triangolo. Come fare :
- costruisci le 3 bisettrici (tagliano un angolo in due parti uguali) o 3 rette perpendicolari [ai lati, passanti per i vertici del triangolo]e le intersechi con Intersezione; quello sarà il centro del triangolo
-prendi un punto mobile, D, su uno dei lati
- crei un segmento (es. di nome g) che unisce il punto D (mobile) con il punto B (vertice del triangolo)
- con centro sul vertice A, con lo strumento Circonferenza dati centro e raggio costruisci la circonferenza e digiti (per la misura del raggio) "g" (nome del segmento)
- ripeti la stessa cosa per il vertice C
- prendi lo strumento Poligono e crei il primo quadrilatero unendo il vertice B del triangolo, il punto mobile, il centro del triangolo e il punto di intersezione della circonferenza con il lato del triangolo. Ripeti la stessa cosa per gli altri 2 quadrilateri
- infine nascondi le circonferenze e dai un po' di colore ai poligoni
Direi che si capisce abbastanza, ancora meglio osservando la costruzione. In tutte le applets si possono visualizzare gli oggetti nascosti con lo strumento Mostra/Nascondi oggetto.
Mancherebbe tuttavia, benché si intuisca per costruzione, la spiegazione del perché i quadrilateri ottenuti siano congruenti.
Voglio infine precisare di aver dato, in entrambe le classi, l’indicazione su come costruire un segmento di data misura mediante Circonferenza dati centro e raggio.
I tre della prima hanno ben saputo sfruttare l’indicazione, perciò, bravi!
Ok... chiudiamo pure con la colorata costruzione, merita, c’è del lavoro seppure statico, di Manuel, che scompone 9 poligoni regolari:
Chiudo con il consueto bravo a chi ha lavorato e/o a chi ci ha provato.
....
Ok, decido di pubblicare, non so se in serata, tarda ormai, arrivino altre soluzioni. I solutori saranno eventualmente inseriti.
Ah, tenersi pronti per la prossima puntata, dal prof. Davide naturalmente.






























Bravi davvero! Stavolta ci avete superati e quasi doppiati, oserei dire. Belle soprattutto le animazioni Geogebra. Stavolta più che mai aiutavano davvero a trovare una risposta al quesito. Infatti noi, con un uso moolto limitato di Geogebra, non ci siamo arrivati.
RispondiEliminaComplimenti a tutti!
Adesso sono in attesa di consiglio (nel senso che sta per iniziare il consiglio di classe) ma stasera conto di pubblicare i prossimi due quesiti. Una roba facile facile!
Ma no, dai, sei troppo buono con noi e troppo poco con ...voi! :-)
RispondiEliminaHo dato una scorsa alle vostre soluzioni, vado a leggervi meglio.
grazie!
...per il mio consiglio han pensato bene di bruciarmi il lunedì, prox, libero :-(