Ahi, signora Geometria,
quanta fatica, quanto ci costi!
Già, direi proprio sia necessario guidare e guidare ancora, perché si sappiano utilizzare e sfruttare proprietà. Ma, sono certa di poter aggiungere: è necessario anche impegnarsi!
Tant’è: il
Quesito 1, geometrico
ha trovato solo quattro solutori, due per classe.
Per la classe prima: Gian Franco, Alessia.
Per la seconda: Bachisio, Pietro S.
Riporto le immagini della costruzione di Pietro, realizzata con GeoGebra, rispettando parallelismi e congruenze di lati e angoli del trapezio, curate in classe proprietà e correttezza di costruzione di un trapezio isoscele. [E, sottolineo anche la cura, in entrambe le classi, della visualizzazione dinamica dell’area di un triangolo che non varia quando non mutino le misure della base e dell’altezza. Da pochi, per l’appunto, saputa sfruttare]
Situazione iniziale:
Situazione risolutiva:
Riporto invece, potendo copincollare, la spiegazione di Gian Franco, adattando la denominazione dei punti:
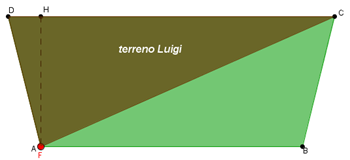
Allora, l'area del triangolo si trova "(b*h): 2". L'area del terreno di Luigi rimane uguale spostando il punto mobile F della costruzione, perché la base rimane sempre la stessa e anche l'altezza rimane la stessa. Quest'ultima affermazione può essere confermata dal fatto che F si muove sempre su un segmento parallelo a CD che è la base del triangolo di Luigi, e quindi se è parallelo mantiene sempre la stessa distanza da CD. Infine se il triangolo ha la stessa base e altezza ho confermato che il triangolo ha sempre la stessa area.
Devo aggiungere che ci sono stati tentativi di soluzioni diverse, con altre linee di separazione, non corredati però da accettabili spiegazioni. Qualcun altro è ricorso al calcolo delle aree con lo strumento “Area” di GeoGebra, ma questa mossa, notare bene una volta per tutte, non è valida!
E passiamo al
Quesito 2
Con i soldi è andata meglio! Non so, con i soldi va sempre meglio...
Hanno dato la risposta corretta, per la prima: Gian Franco, Arianna, Miriam, Alessia, Elisa.
E per la seconda: Gabriele G., Manuel, Bachisio, Davide A., Pierluigi, Pietro S.
Molte risposte sono simili a questa, di Miriam:
I due fratelli hanno 20 soldi a testa...
Il primo compra delle uova e le paga 1 soldo ciascuna, perciò compra 20 uova (quindi spende 20 soldi). Poi le rivende a 2 soldi ciascuna e ricava 40 soldi, da quelli però deve togliere i 20 soldi che ha speso per comprarle, quindi guadagna 20 soldi.
Il secondo , sempre con 20 soldi compra le uova a 2 soldi ciascuna, quindi ne compra 10.
Poi le rivende a 1 soldo ciascuna e ricava 10 soldi, da cui deve sottrarre i 20 soldi spesi per acquistare le uova. Lui purtroppo perde 10 soldi.
In tutto i due fratelli hanno guadagnato solo 10 soldi (20+ (-10) = 10) [ho aggiunto io la parentesi interna, ma già Miriam esegue un piccolo calcolo con i numeri relativi ]
Altri rispondono come Pierluigi. Più o meno:
I due fratelli secondo me guadagnano 10 soldi perché :
Il primo compra 20 uova a 1 soldo e le rivende a 2 soldi ricavando 40 soldi, guadagnandone 20 .
Il secondo compra 10 uova a 2 soldi e li rivende a 1 soldo l'uno perdendo così 10 soldi .
Poi rimettono insieme i soldi (40+10=50) .
Quindi nonostante la perdita subita dal secondo fratello si ritrovano con un guadagno di 10 soldi: 50 (ricavati) –40 (spesi).
Concludo come sempre con i complimenti a chi ha lavorato o tentato. Ma devo considerare con forza: occorre darsi da fare, tanto, con la geometria!
Ps: ho appena letto le soluzioni dei ragazzi del prof Davide: stavolta, come non mai, vi invito (quasi quasi vi ordino! – Dal prof Davide, leggerete, è stato efficace un certo provvedimento...) ad andare a leggere. Dovete andare a leggere!
E, tenetevi pronti per i nuovi quesiti del Sarà mica matematica.


























Be', Prof, la geometria è la bestia nera di molti, si sa (pensare che sarebbe così bella!). Ma mi pare proprio che anche stavolta i ragazzi se la siano cavata niente male. Meritano senz'altro i complimenti.
RispondiEliminaPersonalmente, stavolta più che mai, apprezzo anche che chi ha partecipato lo abbia fatto di sua volontà, senza obblighi. :-)
Quindi ancora complimenti a tutti e alla prossima!
Eh sì, confido, nonostante qualche difficoltà, di riuscire a far apprezzare la bellezza della geometria. Lavoreremo.
RispondiEliminagrazie Prof.
a presto :-)