Sì, decisamente in ritardo
pubblico le soluzioni
Riflessione d’obbligo:
per dirla con il prof Davide, ho voluto anch’io stavolta farmi del male. Tuttavia, è il caso di dire subito che: ci ho provato.
Tant’è che non sono mica arrivate le 35*2 soluzioni attese. Bene: ognuno si è assunto le proprie responsabilità.
Di seguito soluzioni e solutori.
Quesito 1, i numeri palindromi
Si chiedeva il più piccolo numero palindromo divisibile per 15 e il più grande tra i numeri di 4 cifre, palindromo e divisibile per 15.
Per la classe prima, hanno dato le soluzioni corrette e complete (anche di spiegazione): Miriam, Alessia, Giuseppe P., Gian Franco, Daniele. Daniele spiega meglio la seconda risposta. La soluzione della prima parte del quesito, seppure corretta, è frutto di un ragionamento impreciso (chiarito in classe)
Erika risolve la prima parte, Elisa e Arianna, anche loro solo la prima parte e non forniscono la spiegazione. Antonio risponde ad entrambe le domande utilizzando la divisibilità per 15 ma non spiega come ha ragionato per trovare i due numeri. Matteo risponde alla prima domanda, anche lui motivando la risposta solo con la divisibilità.
Un bravo lo meritano tutti (forse, vero giovini?) per aver trovato da soli quando un numero è divisibile per 15 (in prima non si è ancora parlato di Divisibilità)
Per la classe seconda, rispondono in modo soddisfacente: Manuel, Bachisio, Gabriele G., Pierluigi e Pietro S.
Pietro P. e Gian Mario non spiegano le risposte. Così come Davide A.1, che utilizza il criterio di divisibilità ma non dà altre motivazioni. Vincenzo risponde alla prima domanda, senza spiegazione.
Come al solito, copio-incollo le risposte più belle, più ricche e più gustose . Faccio appena un po’ di mix, ma prevale... gli autori si riconoscano!
All'inizio ho pensato che fosse molto difficile ma pensandoci bene ho notato che era molto facile!
Il più piccolo numero palindromo divisibile per 15 è 525.
Prima di tutto un numero divisibile per 15 deve essere divisibile per 5 e per 3.
Per 5 deve finire con 0 o con 5, per 3 la somma delle cifre deve dare 3 o un suo multiplo. Non si può scegliere che finisca con lo zero perché per essere palindromo dovrebbe anche iniziare con la cifra 0 e non avrebbe senso.
Tra tutti i numeri a 2 cifre non ce n’è nemmeno uno che va bene perché tutti finiscono con numeri diversi da 5 tranne il 55 che però non è divisibile per 3. Poi i numeri a tre cifre fino al 400 non possono andar bene perché se iniziano con 1, 2, 3, 4 devono per forza finire con 1, 2, 3, 4 quindi non sono divisibili per 15.
Poi partiamo dal 500 e iniziamo a contare i numeri palindromi che sono 505 e non va bene, 515 e non va bene, poi provo con il 525 e noto che rispetta la richiesta data perché è divisibile per 5, finisce con 5 ed è divisibile per 3, 5+2+5 fa 12 cioè un multiplo di 3 quindi 525 è multiplo di 15 ed è palindromo.
Per la seconda richiesta il più grande dei numeri a 4 cifre, palindromo divisibile per 15 è 5775.
Prendo in considerazione le migliaia del 5000 come nel ragionamento precedente e prendo l'ultimo numero palindromo che è 5995, quest'ultimo non è divisibile per 15 e quindi provo con il penultimo numero che è 5885 e neppure questo va bene. Provo con il terzultimo che è 5775 e secondo il criterio di divisibilità è un numero divisibile per 15.
Quesito 2, bilance e pesi
Bilance non in equilibrio: si chiedeva di ordinare le forme secondo il loro peso, dalla più leggera alla più pesante.
Risolvono e spiegano, per la prima: Alessia, Gian Franco e Giuseppe P. - Miriam, Antonio, Daniele e Matteo non danno troppo chiare spiegazioni.
Per la seconda rispondono: Manuel, Bachisio e Pietro S., bene. Gabriele G. no, non spiega chiaramente.
I ragionamenti più chiari mi sono parsi quelli di Bachisio.
Riporto le figure e... mi tocca scrivere perché il signorino mi dà i foglietti!
Fig. 1:

Considero dapprima come unico peso le coppie b-c e b-a: la coppia b-c è più pesante della coppia b-a (i bracci della bilancia pendono sempre dalla parte delle forme più pesanti). Da questo deduco che c è più pesante di a, poiché b e b hanno uguale peso. Osservando ora solo i piatti destro e sinistro della bilancia, uno per volta, è evidente che b pesa più di c e b pesa anche più di a. Quindi l’ordine, dal più leggero al più pesante è: a < c < b
Fig. 2:

In questa figura i piatti a destra (le due c e le due a) mi fanno capire che c è più pesante di a.
Per confrontare b+c+a con la parte destra, posso togliere una c e una a dai bracci sinistro e destro, così:
b è più pesante di c e a messi assieme. Quindi l’ordine è: a<c<b
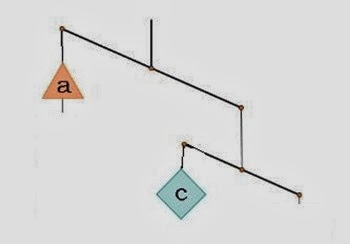
Fig. 3:

Osservando dapprima solo la parte destra noto che b è più pesante di a e c messi assieme. Quindi b è il più pesante. Confronto ora la parte sinistra con la destra: essendo b uguali non li considero. Tolgo poi anche una a da destra e da sinistra, avrò questa situazione:
c è più pesante di a. Quindi l’ordine anche qui è: a<c<b.
Ho finito? Mi pare di sì. Bravo a chi si è impegnato e ribadisco, per chi non ha lavorato: ognuno è responsabile del proprio operato!
Oh, importantissimo! Spettano a noi i nuovi quesiti. Ok, sono pronti. E’ probabile, ma non certo, che siano in linea fra qualche oretta


























Dunque anche la Prof è cascata nella trappola! :-)
RispondiEliminaE tra le righe mi pare di capire che non tutti ne abbiano saputo approfittare... mi sembra una situazione che ho già vissuto! :-)
Allora aggiungo i miei complimenti per tutti quelli che ci hanno provato davvero (e più di qualcuno se l'è cavata egregiamente, mi pare!).
giààà, Davide :-(
RispondiEliminae ho intenzione di insistere... forse qualcuno in più (non oso dire tutti) ha preso coscienza delle conseguenze ! :-)