Ci vuole un albero!

Li abbiamo

costruiti, curati, analizzati e *loro* poi, i ragazzi, strepitosi stavolta, hanno sviluppato il tema...

E a loro è venuto spontaneo “salvare questa lezione”, così hanno detto!

Bene, la salviamo sul blog, certo!

Beatrice, Davide D., Igor, Davì, Davide P. Andrea F., Nanni, Marco N. e Marco D. e Rita

raccontano...

Non faccio sintesi delle relazioni ... perché mi duole!

Relazione di matematica

Ieri pomeriggio abbiamo costruito molti alberi. Come questo:

Durante quell'ora la prof ha sentito pronunciare delle parole matematiche:

divisibile, multiplo, numeri primi, “somma delle cifre”, divisore, sottomultiplo...

e ha fatto finta di niente. Ma oggi ce le ha ricordate …

Ci ha detto che tutte queste parole ci servono per approfondire e per conoscere altre “operatività” in N. Precisamente la DIVISIBILITA' in N...

Se prendiamo in considerazione per esempio 10:3, noi sappiamo che il 10 è il dividendo e il 3 fino a ieri lo chiamavamo divisore, ma oggi non più.

Su questo abbiamo indagato per un po' spiegando molti perché:

• la divisione non ha un quoziente intero

• 10 non è multiplo di 3

• la divisione ha resto ≠ 0

• 10 non è divisibile per 3.

• nella tabellina del 3 non compare il numero 10.

• il 3 non è contenuto nel 10.

Dopo siamo arrivati a dire che: il divisore deve essere contenuto perfettamente nel dividendo. Ma... la prof ci ha chiesto se sapevamo tradurre il termine “perfettamente” in “matematico”. Così dopo un po' di tentativi, anche con l'aiuto della prof, Davì ha detto: un numero è divisore di un altro quando è contenuto nell'altro un numero intero di volte.

Dopo, 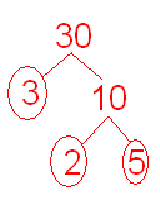abbiamo preso ancora in considerazione l'albero creato da Giuseppe V.

I divisori: 3, 10, 2, 5 sono “contenuti” nel 30 30 = 2*3*5 scomposizione in fattori primi, oppure 30=3*10 scomposizione in fattori

fattori = sinonimo di divisore

La prof ci ha chiesto cosa notavamo nelle ultime foglioline (i numeri all'interno del cerchio), e Stefano ha detto che sono tutti numeri primi, poi la prof ha aggiunto che i numeri primi sono i mattoni della matematica.

Ha chiesto perché secondo noi, “mattoni della matematica” e Laura ha risposto che servono per costruire i numeri, e poi la prof ci ha domandato: se i numeri primi si chiamano così, come si chiamano gli altri? (esclusi i decimali).

E ci ha detto che si chiamano NUMERI COMPOSTI.

//  //

DIVISIBILITA’

Oggi abbiamo iniziato il lavoro continuando quello di ieri “gli alberi”.

Poi la prof ha iniziato ad elencare alcune parole importanti che ha sentito:

Divisibile

Multiplo

Numeri primi

“Somma delle cifre”

Divisore o Sotto multiplo

Abbiamo preso in considerazione Divisore e abbiamo detto che adesso essendo più grandi non dovevamo usare divisore per dire che è un componente della divisione ma …

Abbiamo detto 10:3

3 non divisore e abbiamo risposto:

Giovanni - Perché la divisione non ha un quoziente intero.

Davì – Perché dieci non è un multiplo di tre.

Marco N. – Perché la divisione ha resto ≠ 0.

Davì ha detto che il dieci non era contenuto nella tabellina del tre e allora la prof gli ha detto che la parola contenuto l’avrebbe voluto dire in un’altra frase e allora Marco D. ha detto – Perché nella tabellina del tre non compare il dieci.

E allora Davì ha detto – Perché il tre non è contenuto nel 10.

Ritornando al “ma” di prima, abbiamo detto che Divisore è : Un numero è divisore di un altro quando è contenuto un numero intero di volte.

Ritornando all’ albero: abbiamo indicato quali sono i divisori “di”

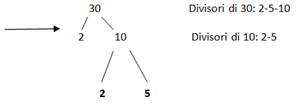
Facendo questo siamo arrivati a dire che: I numeri primi sono i mattoni della matematica questo perché ad esempio

//  //

Sintetico:

Oggi a scuola con la Prof. di matematica abbiamo esaminato un albero e abbiamo elencato alcune parole importanti dette il giorno prima:

- divisibile

- multiplo

- numeri primi

- somma delle cifre

- divisore

- sottomultiplo

Divisore: abbiamo analizzato la parola divisore, trovando tante definizioni con cui spiegare quando un numero che, restando in N, non è divisore di un altro numero.

Siamo arrivati a dire che: un numero è divisore di un altro quando un numero è contenuto nell'altro un numero intero di volte.

Numeri primi: i numeri primi sono i mattoni della matematica, perché formano tutti gli altri numeri che vengono detti composti.

//  //

Relazione di matematica

Tutto è iniziato quando la prof. ieri ha controllato un alberello.

La prof. (curiosona) ha voluto che scrivessimo questo alberello

sul quaderno :

Dopo la prof. ci ha fatto pensare alle parole dette in classe:

DIVISIBILE

MULTIPLO

NUMERI PRIMI

“SOMMA DELLE CIFRE”

DIVISORE O SOTTOMULTIPLO.

Abbiamo detto anche che noi chiamavamo divisore di un numero qualsiasi numero dopo il segno : (diviso) nella divisione.

Era errato perché:

-La divisione non sempre ha un quoziente intero;

-la divisione non sempre da resto uguale a zero;

-non sempre il dividendo è suo multiplo (del divisore);

-non è divisibile per il numero scelto ;

-il divisore non è contenuto nel numero scelto.

Dopo la prof. ci ha posto la seguente domanda:

QUANDO UN NUMERO è DIVISORE DI UN ALTRO?

Quando è contenuto nell’altro un numero intero di volte.

La prof. ci ha detto anche che i numeri primi sono i mattoni della matematica.

//  //

Siamo partiti riscrivendo alla lavagna l’ albero di 30, e scrivendo alcune parole che erano saltate fuori durante le attività, anche se la professoressa ha fatto finta di niente, per esempio:

divisibile;

multiplo;

numeri primi;

“somma delle cifre”;

divisore;

sottomultiplo.

Per prima abbiamo analizzato la parola divisore, noi come l’abbiamo sentito abbiamo detto che era il 2° termine della divisione, ma la prof. ci ha detto che solo fino a ieri potevamo dare quella spiegazione, allora ci ha fatto questi esempi:

10/3: fino ieri andava bene, 3 era il divisore

10/3: 3 non è divisore di 10,

e ci ha detto che questo faceva parte del grande racconto della DIVISIBILITA’.

Allora ci ha chiesto perché 3 non è divisore di 10, e noi abbiamo risposto così:

1) la divisione non ha un quoziente intero;

2) 10 non è multiplo di 3;

3) la divisione ha il resto non uguale a zero 0;

4) 10 non è divisibile per 3;

5) Nella tabellina del 3 non compare il 10.

Dopo che abbiamo detto perché il 3 non è un divisore di 10 ci mancava di dire come fa un numero ad essere divisore di un altro, un nostro compagno ha detto:

UN NUMERO E’ DIVISORE DI UN ALTRO QUANDO E’ CONTENUTO PERFETTAMENTE NELL’ ALTRO

Ma non andava bene, dovevamo rendere più matematico quel perfettamente, allora abbiamo cercato di aggiustarlo, e poi siamo arrivati a dire la regola:

UN NUMERO E’ DIVISORE DI UN ALTRO QUANDO E’ CONTENUTO NELL’ ALTRO UN NUMERO INTERO DI VOLTE

Dopo aver detto la regola un nostro compagno ha notato che le ultime “foglioline” dell’ albero erano numeri primi, la prof infatti ci ha detto che i numeri primi erano i mattoni, o gli atomi, della matematica, e ci ha chiesto che cosa significava questa frase, e uno di noi ha detto perché siccome i mattoni costruiscono la casa, i numeri primi costruiscono gli altri numeri.

Quindi se i numeri primi sono gli atomi, gli altri numeri sono le molecole, e quindi la matematica è la materia. (! )

//  //

Divisibilità

Siamo partiti da una scomposizione di un numero ad albero:

fino a ieri noi chiamavamo divisore il secondo termine della divisione (dividendo e divisore), ma oggi abbiamo imparato che per divisore si intende anche un’altra cosa…….

La prof ci ha fatto l’esempio di 10 / 3 e ci ha cancellato il 3 dicendoci che lui non era divisore di 10, allora noi all’inizio eravamo un po’ meravigliati ma poi abbiamo dato una serie di risposte e abbiamo detto che non era divisore perché:

la divisione non ha quoziente intero

10 non è multiplo di 3

La divisione ha resto ≠ 0

10 non è divisibile per 3

Nella tabellina del 3 non compare il numero 10

Il 3 non è contenuto nel 10

Da tutte queste risposte siamo riusciti a formarne una unica con gli stessi significati delle altre, però più precisa:

un numero è divisore di un’ altro quando è contenuto nell’ altro un numero intero di volte

Inoltre pensando alla lezione precedente la prof ci ha ricordato che abbiamo pronunciato 6 parole per noi oggi importanti:

DIVISIBILE

MULTIPLO

NUMERI PRIMI

“SOMMA DELLE CIFRE”

DIVISORE

SOTTOMULTIPLO

Infatti ritornando all’ albero ci accorgeremo ad esempio che 3, 10, 2, 5 sono divisori di 30, cioè sono contenuti un numero intero di volte

Ci siamo accorti che 30 si può scomporre in diversi modi,

però le ultime cifre sono sempre le stesse.

Sono anche chiamati numeri primi

I numeri primi sono i mattoni della matematica,vengono chiamati “mattoni” perché formano i numeri.

Mentre il 30 è chiamato numero composto.

30=2*3*5 - è una scomposizione fattori primi

30=10*3 - è una scomposizione fattori

//  //

Immagine da scanner perché consegnata stampa

(Davì, avete fatto tutto voi! Grazie a voi!)

Infine...

qualcuno, preso dalla foga nel rendicontare,  è andato avanti..

Oggi abbiamo iniziato la lezione disegnando una struttura ad albero.

Poi abbiamo elencato i termini che ieri abbiamo utilizzato (che però la prof ha fatto finta di non sentire ):

divisibile, multiplo, numero primo, somma delle cifre, divisore o sottomultiplo.

Dopo un po’ abbiamo dato il nome a questo argomento, l’abbiamo chiamato:

divisibilità ( nell’insieme N )

il primo termine che abbiamo spiegato è:

Divisore

la parola divisore la usavamo fino a ieri ma oggi no perché abbiamo capito che l’insieme N non è sempre chiuso per la divisione, ognuno di noi ha dato un’opinione diversa :

Giovanni: la divisione non ha un quoziente intero

Davi: 10 non è un multiplo di 3

Marco : perché la divisione ha resto diverso da 0

Andrea F: perché 10 non è divisibile per 3

Marco D: nella tabellina del 3 non compare il 10

Davi: il 3 non è contenuto nel 10

La prof ci ha fatto una domanda :

quindi cosa vuol dire divisore?

Un numero è divisore quando è contenuto nell’altro un numero intero di volte.

Cosi abbiamo dato all’albero un nuovo nome è l’abbiamo chiamato scomposizione ad albero. Che consiste nello scomporre un numero scelto in fattori primi o anche in numeri composti.

Ci sono delle regole note come criteri di divisibilità che dicono se un numero è divisibile ad un altro senza fare una divisione.

I criteri di divisibilità possono essere per 10 per 100………

Perché un numero sia divisibile per 10 deve finire per 0

Criterio di divisibilità per 2 e per 4

Perché un numero sia divisibile per 2 l’ultima cifra deve essere pari o 0 mentre un numero divisibile per 4 le ultime due cifre a destra devono formare un multiplo di 4.

Criterio di divisibilità per 5 e per 25

Un numero è divisibile per 5 o 25 quando termina con 5 o con 0 o con due zeri.

Criterio di divisibilità per 3 e per 9

Un numero è divisibile per 3 quando la somma delle sue cifre e è un multiplo di 3; è divisibile per 9 quando la somma delle sue cifre forma un multiplo di 9.

Numeri primi

I numeri primi sono i mattoni della matematica, poi Laura ha dato le spiegazioni :

i numeri primi compongono i numeri.

I numeri primi che compongono trenta sono:

30=2*3*5

2 3 5 li abbiamo chiamati fattori primi, mentre il secondo in fattori: 30 = 3 * 10

Un numero è primo quando si può dividere per se stesso e per uno

Si possono anche costruire delle tavole:

· Si scrivono i numeri fino a 100

· Si cancellano tutti i numeri pari a parte il due.

· Fra i rimanenti si cancellano tutti i multipli di tre, i multipli di cinque e cosi via fino ad avere eliminato tutti i numeri composti.

Questo si chiama crivello di Eratostene, uno scienziato greco.

Articoli correlati per categorie