Erica, Letizia e Maria Chiara,
tornano a scrivere! Hanno scritto singolarmente, bene tutte e tre. Riporto la sintesi delle tre relazioni.
Prodotti notevoli, potenze di binomi e anche...
Dopo aver acquisito sicurezza nei vari calcoli con monomi e polinomi, eccoci immersi nell’elevamento a potenza di binomi.
La prof ci chiede di risolvere le seguenti espressioni:
Quindi deduciamo che $(a+b)^2 = (a+b)(a+b)$, un prodotto che sappiamo ben risolvere. Applicando la proprietà distributiva e riducendo i termini simili, otteniamo:
La prof ci ha invitato a iniziare a fare delle considerazioni o a cercare di trovare delle regolarità nei polinomi ottenuti.
Intanto ci ha fatto notare che, mentre ci chiedeva i risultati, sapeva già che il polinomio sarebbe stato composto da tre termini.
Prendendo in considerazione la terza espressione $(-4ab+3a^2b)^2$, abbiamo notato che il primo termine del risultato $(16a^2b^2)$ era il quadrato del primo termine dell’espressione (-4ab), il secondo termine del risultato $(-24a^3b^2)$ era il doppio prodotto del primo per il secondo $[2(-4ab*3a^2b)]$ e che il terzo termine $(+9a^4b^2)$ era il quadrato del secondo $(3a^2b)$.
Ovviamente la stessa cosa succedeva anche per le altre due espressioni, così la prof è intervenuta dicendo che eseguendo questi particolari prodotti potevamo farne delle “regole generali”. Questi prodotti infatti prendono il nome di prodotti notevoli e per risolverli possiamo evitare i consueti passaggi algebrici.
La regola da seguire per calcolare il 1° prodotto notevole ovvero il quadrato di un binomio è la seguente:
- quadrato del primo termine;
- doppio prodotto del primo termine per il secondo;
- quadrato del secondo termine
Successivamente abbiamo fatto la medesima analisi anche con il cubo di un binomio. Abbiamo sviluppato:
E siamo arrivati alla conclusione che i passaggi necessari per calcolare il cubo di un binomio sono:
- cubo del primo termine;
- triplo prodotto del quadrato del primo termine per il secondo;
- triplo prodotto del quadrato del secondo termine per il primo;
- cubo del terzo termine
Ma… non è ancora finita…
La prof ci ha detto di concentrare la nostra attenzione sui coefficienti numerici dei risultati del quadrato e del cubo di un binomio, e così abbiamo fatto:
$(a+b)^2=1a^2+2ab+1b^2$
$(a+b)^3=1a^3+3a^2b+3ab^2+1b^3$
Non sono per caso 1 2 1 e 1 3 3 1 ? Non ci ricorda qualcosa?
Dopo qualche istante, ci viene in mente il triangolo di ... di... sul quale avevamo tanto lavorato all’inizio dell’anno... di Tartaglia!
Ebbene si, la matematica ci stupisce ancora una volta, parliamo di nuovo del triangolo di Tartaglia.
Riportiamo alla lavagna alcune righe per provare a scoprire come utilizzarlo per calcolare in maniera ancora più rapida le potenze dei binomi [siamo stati bravi con le prime due righe!]:
Abbiamo anche notato che, nelle potenze di binomi, es.$(a+b)^3$, i monomi sono ordinati in modo decrescente rispetto alla lettera a e crescente rispetto alla b:
$a^3b^0+3a^2b^1+3a^1b^2+ a^0b^3$
Quindi abbiamo provato a calcolare $(a+b)^4$ servendoci solo della sequenza dei numeri del triangolo di Tartaglia e della regolarità degli esponenti:
$(a+b)^4=a^4+4a^3b+6a^2b^2+4ab^3+b^4$
Quindi, possiamo ...
sviluppare qualsiasi Potenza di un binomio!
Comodo il Triangolo di Tartaglia!


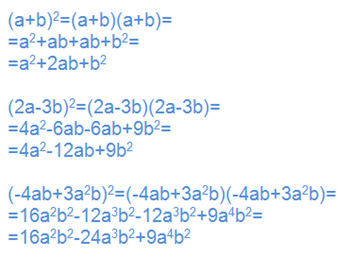


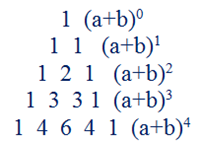
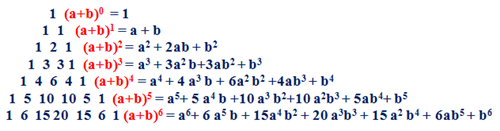
























Nessun commento:
Posta un commento
I vostri commenti sono graditissimi, l'interazione è molto utile!
Non ci piace però comunicare con "anonimi". Vi preghiamo di firmare i vostri messaggi.
Come fare:
Cliccare su Nome/URL.
Inserire il vostro nickname nel campo "nome".
Lasciate vuoto il campo URL se non avete un blog/sito.
Grazie!