Due a settimana …_16, le soluzioni

Infine, le soluzioni del

Due a settimana …_16

Infine, quasi! Si tratta delle penultime soluzioni dei giochi per quest’anno scolastico. E’ invece il nostro ultimo Due a settimana…, l’ultima puntata Sarà … mica matematica. E sarà pure il numero 40, complimenti al prof Davide!

Ma andiamo con le soluzioni.

Quesito 1, il 2016° numero

Solutori e soluzioni per la classe prima:

Andrea, essenziale come sempre:

il duemilasedicesimo numero è l'89 perché è l'ottavo, poi il sedicesimo, il ventiquattresimo ecc. quindi devo solo sapere se 2016 è multiplo di 8 e lo è secondo 252.

Roberta, invia tutto il lavoro che la porta alla soluzione:

2016
2^2 + 0^2 + 1^2 + 6^2 = 41
4^2 + 1^2 = 17
1^2 + 7^2 = 50
5^2 + 0^2 = 25
2^2 + 5^2 = 29
2^2 + 9^2 = 85
8^2 + 5^2 = 89
8^2 + 9^2 = 145
1^2 + 4^2 + 5^2 = 42
4^2 + 2^2 = 20
2^2 + 0^2 = 4
4^2 = 16
1^2 + 6^2 = 37
3^2 + 7^2 = 58
...

Arrivata a questo punto ho capito che, dal numero 89 in poi, le somme si ripetevano all'infinito, quindi ho verificato scomponendo un altro po' di numeri.

Poi ho fatto -> 2016° numero : 8 (numeri che si ripetono) = 252 n° volte che si ripete la successione di numeri (sempre uguali), quindi la successione si ripete un numero intero di volte.

Ho considerato che dagli otto numeri che si ripetono devo sottrarre 7, i numeri della serie che non si ripetono. Quindi il 2016° numero è 89.

Paola:

Il 2016° numero è l'89 perché si ripete ogni 8 volte, quindi si ripete per i multipli di 8, e il 2016 è un multiplo di 8 perché 2016/8 = 252.

Davide:

Dopo aver trovato che 89, 145 , 42 , 20 , 4, 16, 37 e 58 si ripetono all'infinito, ho riflettuto e ho capito che il 2016° numero è 89 perché è 8° numero della serie e 2016:8=252.

Antonio:

ho iniziato continuando la serie. Mi sono ritrovato 2 volte l'89 e quindi la serie continuerà all'infinito così: 89,145,42,20,4,16,37,58,89... Deduco che il 2016 numero è 89 perchè ogni 8 numeri c'è l'89 quindi l'800esimo numero sarà l'89, il1600esimo numero sarà l'89, il2000esimo numero sarà 89 e il 2016esimo numero sarà 89. – Va beh, ma perché stare a eseguire una divisione? – dice Antonio!

Elena:

Guardando bene la successione ho visto che questa successione assomiglia ai numeri felici [e brava. Li avevamo visti QUI. Il 2016 non lo è, vero Elena?]. Dopo essermene accorta ho continuato:

2^2+5^2=29
2^2+9^2=85
8^2+5^2=89
8^2+9^2=145
1^2+4^2+5^2=42
4^2+2^2=20
2^2+0^2=4
4^2=16
1^2+6^2=37
3^2+7^2=58
5^2+8^2=89

Ho visto che il n° 89 si ripete, il 2016° numero è 89 [Ma Elena proprio non riesce a spiegare il perché ]

Sara:

Ho continuato la successione finché ho notato che l'89 si ripete all'ottavo numero, quindi il 2016esimo numero è 89 perché ho fatto 2016:8=252, ogni 8 numeri c'è l'89.

Yuri: mi consegna la soluzione su foglietto e io NON trascrivo! La sua risposta è comunque esatta e buono il ragionamento.

Marta C.:

Continuando la successione, ho notato che ogni 8 numeri la successione si ripete. Perciò ho fatto 2016/8=252. Quindi il 2016[esimo] numero sarà 89.

Solutori e soluzioni per la classe terza:

Alessia: dopo astrusi ragionamenti, riesce a concludere semplicemente!

Il 2016esimo numero è 89.

Per trovarlo ho diviso 2016 per il numero di serie dove appare per la prima volta l'89, ovvero 8, ottenendo così 252 che significa che l'ottavo numero, ovvero 89, si ripete 252 volte per raggiungere il 2016esimo numero.

GianFranco: oh, ma questi di terza mi diventano complicati, anche Gianfri arzigogolava, poi finalmente:

Riflettendo un po’ ho pensato che siccome il numero che si ripete nella serie è 89, l'ottavo il numero della serie, e si ripete ogni otto numeri, non dovevo sottrarre niente perché non aveva senso [per l’appunto! Ma anche perché giungevate a conclusioni errate] allora ho diviso direttamente il 2016 per 8 trovando 252, cioè il numero di volte che l'89 si ripete per arrivare al 2016esimo che è appunto 89.

Miriam:

per trovare la soluzione, con il solito metodo, mi sono calcolata un po’ di numeri:
primo numero: 2016
secondo numero: 41
terzo numero: 17
quarto numero: 50
quinto numero: 250
sesto numero: 29
settimo numero: 85
....
continuando, ho notato che dall'ottavo numero parte una serie di 8 numeri (in quest'ordine: 89; 145; 42: 20; 4; 16; 37; 58) che si ripetono all'infinito...
perciò, per trovare il 2016esimo numero, ho diviso 2016 per 8, ottenendo il numero di volte che la sequenza si ripete, pari a 252. Da questo ho potuto dedurre che il 2016esimo numero è 89.

Antonella:

Il duemilasedicesimo numero sarà 89. Ho trovato questo risultato continuando la serie fino a trovare il numero 89 una seconda volta, facendo quindi 2016:8 (perche l'89 è nell'ottava posizione nella serie)= 252 ovvero quante volte si ripete l'89.

Elisa:

ho continuato la serie fino ad un certo punto e ho notato che partendo dall'ottavo numero della serie, che è 89, i numeri si ripetono. Mi chiedeva quale fosse il 2016° numero quindi ho fatto 2016:8=252 che è il numero di volte che 89 si ripete, quindi il 2016° numero è 89.

Giuseppe P:

Continuando la serie ho notato che ogni 8 numeri compariva l’89.
2016:8=252
Quindi 2016 è un multiplo di 8 e dunque il 2016° numero sarà 89.

Soluzioni Quesito 2, la stella

Per la prima:

Andrea e Paola inviano due soluzioni

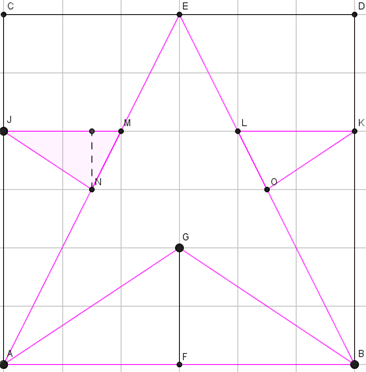
Questa la costruzione (di Paola) su geogebra per la prima soluzione

Paola scrive:

L'area della stella è di 350 mm^2. Ho considerato il triangolo ABE e ho calcolato l'area (6*6/2=18) [Paola calcola in unità-quadrettatura], poi ho calcolato l'area del triangolo ABG (6*2/2=6). Quindi l'area di AGBE è: 18-6=12. Poi ho calcolato l'area di JMN e di LKO (che sono equivalenti) =(2*1/2)*2=2. Per trovare AGBOKLEMJN faccio 2+12=14. Ma siccome i quadratini sono di 25 mm^2 faccio 14*25=350mm^2.

Andrea invece:

L'area della stella è 350mm^2 perché:

ABE [modifico io il nome dei vertici dei poligoni…] è uguale a 450mm^2 perché ogni lato del quadrato è 30 mm;
all'area del triangolo tolgo 150mm^2 che è l'area di AGB e aggiungiamo 50mm^2 che è la somma delle aree dei due triangoli JMN e LKO. Quindi: 450mm^2-150mm^2+50mm^2=350mm^2

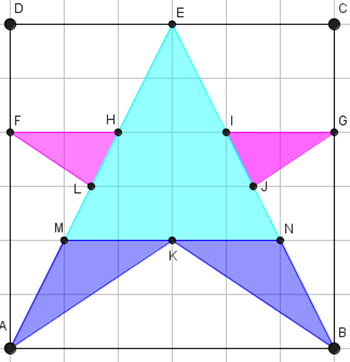
La seconda loro soluzione, costruzione sempre di Paola, eh, cura di più!

Paola dice:

Ho calcolato prima l'area del quadrato(ABCD): 6*5 mm (lato del quadratino)= 30 mm, lato del quadrato. 30*30 = 900 mm^2.
Poi ho calcolato l'area del triangolo AJN: 4*5 mm = 20, base del triangolo, 1,5*5 mm = 7,5 mm, altezza. 20*7,5/2 = 75 mm^2.
Il triangolo BKO è equivalente quindi area= 75 mm^2 e somma 150 mm^2.
Dopo ho trovato l'area del trapezio CEJM: 2*5 mm = 10 mm, base minore, 3*5 mm = 15 mm, base maggiore, 10 mm l’altezza. (Base minore + base maggiore)*altezza/2 = (15 + 10)*10/2 = 125 mm^2.
Il trapezio DEKL è equivalente, quindi faccio direttamente CEJM*2 = 125*2 = 250mm^2.
L’area del triangolo ABG è: 30 mm * 10 mm/2= 150 mm^2.
Infine per trovare l'area della stella: 900 mm^2 - (150 mm^2 + 250 mm^2 + 150 mm^2) = 900mm^2-550mm^2 = 350 mm^2.

Andrea:

Lato di ogni quadratino: 5mm.

AJN e BKO sono uguali, quindi con la stessa area, io so la base e l'altezza, la base è 20mm e l'altezza di 7,5mm, quindi faccio 20*7,5/2=75mm^2 ma visto che i triangoli sono due la raddoppio e diventa 150mm^2.
CEJM e DEKL sono due trapezi rettangoli con la stessa area, per trovarla devo fare (base maggiore + base minore)* altezza /2 quindi (10+15)* 10/2= 125 che devo moltiplicare *2 visto che i trapezi sono due.
ABG ha un'area di 150mm^2, la trovo facendo: base= 30mm^2* altezza= 10/ 2= 150mm^2, quindi l'area della stella è 350mm^2 visto che 900mm^2 (area del quadrato) – (150mm^2+250mm^2+ 150mm^2)= 350mm^2.

Roberta. La sua costruzione:

Il suo ragionamento:

E a proposito di ragionamenti complessi! Voglio mostrare la prima soluzione di Roberta: risparmiando la descrizione, ecco la sua costruzione, direi abbastanza esplicativa:

Beh, un lavoraccio, come non riconoscerlo. In pratica Robi trova l’equivalenza della stella con 1/3 del quadrato sommato all’area del rettangolo ottenuto alla destra della costruzione.

Antonio:

considerando i quadratini la cui superficie è 25 mm², i lati sono di 5 mm. Ho diviso il quadrato in zone che potevo calcolare facilmente e sono:
A=triangolo scaleno
B=triangolo scaleno
C=quadrato
C1=triangolo rettangolo
D=quadrato
D1=triangolo rettangolo
E=triangolo isoscele.

Yuri, soluzione come quella di Antonio, la sua coloratissima costruzione:

Sara: soluzione Antonio – Yuri, fa qualche errore sulle misure, che poi corregge ma non corregge le aree relative!

Elena: soluzione seconda soluzione Paola-Andrea, con trapezi e triangoli esterni alla stella.

Marta C: e va bene pubblico la sua non chiara, né mai chiarita soluzione!

Eseguo: 25mmq*36quadrati=900mmq, poi: 25mmq*22quadrati=550mmq
Infine 900-550=350mmq=superficie stella.

Come Marta individui i 22 quadrati esterni alla stella si aggiunge ai problemi irrisolti della matematica!

E questo vale anche per Davide:

… trovo l’area di tutti i quadratini bianchi figura bianca per figura bianca. Trovo la somma di tutti i quadratini: 4+2+4+1+2+2+2+2+1+2=22

Alla mia richiesta di chiarimenti:

Provo a spiegarglielo meglio: allora, io riesco a formare i 22 quadratini prendendo i terzi o i quarti di quadratino e formandolo intero (me lo spiega meglio ma io continuo a non capire, sigh! Ed è lui che ci rinuncia, ri-sigh!)

Elisa invia la soluzione, simil Antonio-Yuri, con risultato corretto ma con qualche errore nelle misure…

Per la terza, i solutori:

GianFranco: soluzione 2 Andrea-Paola

Alessia: idem

Antonella: idem

Elisa: idem

Giuseppe P.: idem, ma allega una bella costruzione:

Miriam: sua costruzione:

Bene, mi pare di aver detto tutto!

Come sempre Bravo a chi ha lavorato bene, a chi ha lavorato meno bene, e anche a chi ha provato ma non è riuscito.

Il prossimo, ripeto, ultimo appuntamento per quest’anno, dal Prof Davide.

Articoli correlati per categorie