Ed ecco le soluzioni
dei giochi per le vacanze di Natale. Sono trascorse ben tre settimane, non vi ho trovati in piena forma nelle risposte. Non tutti almeno. Molti di voi, in più di un quesito, hanno dovuto ri-tentare! Sarà proprio perché sono trascorse ben tre settimane? Troppe!? E il clima natalizio non si confà ai giochi matematici? Ma pure a tanto altro… non si confà, eh eh.
Quesito 1 treni, fermate e…
Per la classe prima risolvono: Roberta, Maria, Valentina, Andrea, Paola, Elisa, Yuri, Aurora, Marta C., Antonio, Marta D., Sara, Luca, Margherita. Martina, che può aver lavorato con Sara, ma non si è ben capito, non ha comunque corretto il risultato errato.
Per la terza: Antonella, Alessia, Miriam, Gian Franco, Elisa, Giuseppe P.
Le risposte sono tutte abbastanza simili, in sintesi:
ho calcolato inizialmente la metà di 114 quindi 57. Ho diviso questo numero per la differenza dei passeggeri in uscita dal treno e quelli in entrata ad ogni fermata, quindi per 7. Il numero più vicino alla metà di 114 che sia divisibile per 7 è il 56. Quindi 56:7=8. Dopo 8 fermate il numero dei passeggeri rimasti è il più vicino possibile alla metà di quello iniziale.
In alternativa, è stato trovato il numero che moltiplicato per 7 si avvicina di più a 57.
Qualche solutore della prima, forse volendo dedicare più tempo , dopo aver diviso per 2 il 114, ha eseguito delle sottrazioni successive da 114: 114-13+6=107; 107-13+6=100; etc … fino ad arrivare a 58. Lo ha fatto per 8 volte, infatti: da tutto ciò deduco che dopo 8 fermate il numero di passeggeri rimasti è il più vicino possibile alla metà dei passeggeri iniziali.
[Oh, abbiamo già avuto occasione, giusto in questi giorni, di verificare che la divisione può considerarsi una sottrazione ripetuta di sottraendi uguali. Ho invitato a richiamare alla mente certe risposte ai quesiti e, sì, ho visto qualcuno annuire … ]
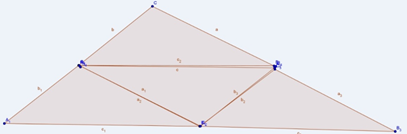
Quesito 2 il triangolo 4 volte più grande
Ebbene, il 4 volte più grande ha dato il suo bel daffare! Sono state date due differenti risposte.
Alcuni solutori, indistintamente, e della prima e della terza, hanno interpretato come 4 volte più grande l’area del triangolo.
Altri invece hanno interpretato, correttamente, come 4 volte più grandi i lati del triangolo.
Evidentemente solo in pochi hanno letto con attenzione la mia considerazione sul quesito. Tuttavia ho deciso di prendere per buone entrambe le interpretazioni poiché la sola formulazione del problema, richiedendo il triangolo 4 volte più grande, poteva pure dare luogo all’equivoco.
Ma pongo a tutti la domanda: se la richiesta fosse stata la costruzione di un triangolo 3 volte più grande, sareste riusciti a triplicare l’area utilizzando come “piastrella” il triangolo dato (ma anche uno diverso)?
Eh, non posso negare di aver provato una certa delusione da parte dei (pochi) solutori della classe terza: solo di recente si era parlato di similitudini e omotetie! Il n° di volte più grande era stato considerato nei suoi diversi aspetti: lati, perimetri, aree… E sia, come si diceva sopra, la concentrazione durante le vacanze era carente.
Veniamo alle soluzioni e i solutori.
Per la prima: Roberta, Paola, Elisa, Andrea, Aurora, Luca, Marta C. Yuri, Sara e Martina (che inviano separatamente la stessa risposta, affermano anche di aver fatto tutto su geogebra, ma non presentano alcuna costruzione. Neppure su invito a …), Antonio invia la risposta senza alcuna spiegazione. E non va bene!
Roberta, Paola e Aurora hanno moltiplicato per 4 le misure dei lati del triangolo.
Roberta dice:
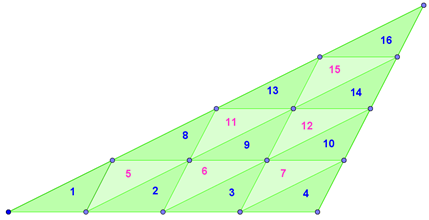
Sì, è possibile costruire un triangolo 4 volte più grande di quello dato. Io ho utilizzato in tutto 16 triangoli.
Per ottenere questo risultato innanzitutto ho riflettuto attentamente sul consiglio datoci dalla prof. e mi è tornato in in mente un esercizio che avevamo trovato sul libro [Si tratta di un esercizio sulla variazione del prodotto al variare dei fattori in una moltiplicazione, della quale sul testo avevamo commentato l’interpretazione geometrica]
Con un ragionamento alquanto complicato, Roberta pasticcia in un primo momento con la costruzione su Geogebra, tracciando in maniera imprecisa l’altezza del triangolo di partenza [ma si può ben scusare, il triangolo è ottusangolo e ancora in prima non abbiamo parlato di altezze. In compenso, sollecitata via e mail a scoprire, ha imparato a costruire le altezze!]
Scrive successivamente:
Se quadruplichiamo la base [e anche gli altri lati], quadruplica anche l’altezza del triangolo. Quindi la formula per calcolare l’area sarà: 4*b*4*h/2. Semplifico la formula utilizzando la proprietà commutativa: 4*4*b*h/2.
Quindi la formula finale è: 16*b*h/2
Una volta eseguito questo ragionamento ho costruito la figura per accertarmi del risultato.
Paola scrive:
il n° di triangoli che ho dovuto usare per formare un triangolo 4 volte più grande del triangolo principale sono 16. Su geogebra ho prima costruito un triangolo con un lato da 4, uno da 3 e uno da 6, poi ho costruito un triangolo con un lato da 16, uno da 12 e uno da 24 (cioè 4 volte più grande). Dopo ho posizionato il triangolo minore in un punto del triangolo maggiore e ne ho copiato e incollato degli altri. Da lì ho capito che erano 16.
Aurora:
ho riprodotto il triangolo poi ho moltiplicato le sue misure *4. Per vedere quanti triangoli mi servono per piastrellare ho ruotato [manualmente?] i triangoli più piccoli in modo che combaciassero. Quando ho finito ho contato i triangoli e sono 16
Elisa e Andrea propongono le due soluzioni.
La prima dice: usando 3 triangoli uguali ho trovato un triangolo 4 volte piu grande, ho usato 3 triangoli, il quarto triangolo (cioe quello al centro) lo ricavo accostando i 3 triangoli
Poi aggiunge: dopo aver letto di nuovo la domanda ho pensato di moltiplicare per quattro i lati e ho scoperto che al suo interno ci sono sedici triangoli.
Andrea dice di aver pensato ad entrambe le soluzioni e invia le due costruzioni:
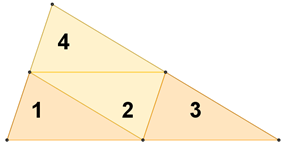
Luca, Marta C. e Yuri quadruplicano l’area, Sara e Martina e Antonio i lati ma non spiegano...
Comunque: e bravi i primini!
Per la terza, i solutori: Alessia, Antonella, Gian Franco, Miriam, Giuseppe P.
Sarà forse più pigra la terza? Chissà… pure tenuto conto del numero inferiore di alunni. Ah!
Alessia, Gian Franco e Antonella quadruplicano in un primo momento l’area e, solo dopo osservazione della prof., aggiustano il tiro e pensano all’omotetia di rapporto 4.
Gian Franco invia la costruzione con l’omotetia e, sullo sfondo, la visualizzazione dei 16 triangoli ottenuti con una serie di traslazioni e rotazioni (ma la costruzione è piuttosto contorta).
Miriam e Giuseppe risolvono quadruplicando l’area.
Giuseppe scrive:
Secondo me la regola alla quale si fa riferimento è quella della similitudine.
Il rapporto tra le aree del primo e del secondo triangolo è di 1/4 (rapporto similitudine tra le aree ) e quindi il rapporto di similitudine dei lati è 1/2 , secondo la regola che afferma che il rapporto fra le aree di due poligoni simili è uguale al quadrato del rapporto di similitudine . Abbiamo affiancato a quello dato altri 3 triangoli uguali come si può vedere nell'immagine sotto
Giuseppe, e tutti: ripensate all’osservazione di cui sopra….
Quesito 3 i cubi colorati “bene” quando:
• La faccia rossa opposta alla gialla;
• La faccia blu opposta alla arancione;
• La faccia verde opposta alla celeste.
Risolvono per la prima: Roberta, Maria, Valentina, Andrea, Paola, Elisa, Yuri, Aurora, Marta C., Antonio, Marta D., Sara e Martina Luca, Margherita.
Per la terza: Antonella, Alessia, Miriam, Gian Franco, Elisa, Giuseppe P.
Qualche solutore della prima risponde correttamente alla prima domanda ma non alla seconda. Anche qualcuno dei solutori terzini, inciampa nella seconda domanda!
Le soluzioni sono simili, in sintesi:
i cubi colorati bene secondo i fratellini sono l'1 e il 5 perché hanno rispettivamente la faccia blu opposta all'arancione e così via…
Ripiegando i 5 cubi [i 5 sviluppi!] quelli uguali sono il primo e il quinto dato che erano stati colorati bene (secondo i fratellini)
Io penso che nessuno abbia ripiegato sviluppi. Male!
Anche stavolta mi pare ci sia tutto. Osservazioni eventuali, ma soprattutto, approfondimenti e discussioni in classe. Uhm, ehm!
Non mi resta che confidare in migliori performances per i prossimi giochi che troveremo dal prof. Davide.
E, in ogni caso, bravo a chi ha lavorato!




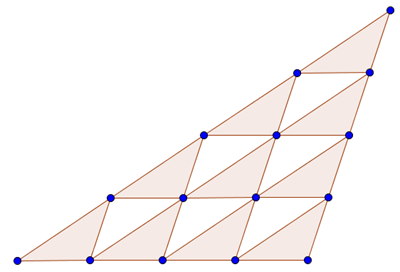



























Le vacanze fanno male, l'ho sempre detto, io :-D
RispondiEliminaPerò, prof, anche stavolta qualche buono spunto c'è, non si può negare. Allora mi associo ai complimenti ai primini e a tutti quelli che si sono dati da fare!
Per parte mia ho commesso l'errore imperdonabile di assegnare il lavoro sui quesiti come compito per le vacanze. Con il risultato che adesso è come se avessi tre pacchi di verifiche da correggere. Spero di finire entro stasera ma temo che la pubblicazione delle nostre risposte sarà rimandata a domani! Però mi sento già di anticipare che la grande quantità non è sinonimo di grande qualità... e questo conferma che le vacanze fanno male!
A proposito: quanto manca a Pasqua? :-D
Ciao Giò mi sei mancata! Matematica e colori, un bellissimo connubio :-) Buon anno, bello ritrovarti sempre così attiva e piena di rispetto per i tuoi ragazzi! Un bacione
RispondiEliminaDavide,
RispondiEliminagià già, le vacanze! Pasqua poi, così lontana... :-( ihihih
E tu correggi con calma, non c'è fretta. Noi dobbiamo ripassare!
Grazie.
Nicone, grazie! Buon anno anche a te.
RispondiEliminaMmm, sono attiva... sono pure stanchissima :-)
Abbraccione!