Ecco le nostre soluzioni del
Quesito 1 la media dell’8!
Per la classe prima hanno risolto correttamente: Antonio, Marta C., Elena, Andrea, Paola, Yuri, Aurora, Roberta e Luca (benvenuto fra i solutori, Luca )
Sintetizzo le soluzioni:
Il voto minimo della terza verifica è 7.
Le informazioni erano:
6 voto della prima verifica;
9 voto della seconda verifica;
8 voto di media desiderato;
4 n° verifiche del primo quadrimestre;
Non esistono i mezzi voti.
Per trovare questo risultato mi sono servita della media aritmetica: ho fatto 8*4=32. 32 punteggio totale per riuscire ad avere 8 di media.
Ho sommato i voti delle prime due verifiche: 6+9=15. Poi da 32 ho tolto 15: 32-15=17. 17 punteggio rimanente per poter avere 8 di media.
Nella terza verifica il prof. Davide potrebbe aver preso 8 o 7 e nella quarta 9 oppure 10. Ma si chiede il voto minimo della terza verifica, quindi è 7.
Per la terza, risolvono: Alessia, Gian Franco, Antonella, Miriam e Giuseppe P.
Sintetici tutti:
per avere 8 di media nelle 4 verifiche il prof deve raggiungere la somma di 32;
la somma delle prime due verifiche è 15;
i restanti 17 punti dovrà totalizzarli con un voto minimo di 7 e con il massimo della valutazione, cioè 10.
Quesito 2 la scala dei quadratini
Solutori per la prima: Elena, Paola, Yuri, Antonio, Andrea, Roberta, Marta C., Aurora, Maria, Luca, Sara e Valentina.
Quesito decisamente stimolante! Ehmm ... qualcuno si è divertito perfino a disegnare i 37 quadratini in scala, insomma insomma e che faticaccia!
La spiegazione di Yuri è tuttavia in qualche modo sorprendente:
ho disegnato i quadrati e ho contato i lati del perimetro: sono arrivato a 76. Poi ho anche scoperto la formula e cioè n*2+2. Mi ha confermato la risposta pure il disegno che c’era sul post perché avevo 5 quadrati e perimetro di 12, quindi 5*2+2=12.
Yuri mi spiega, in un secondo momento, che ha trovato la formula considerando che nei 37 quadrati, 2 lati sono visibili per tutti ma del primo e dell’ultimo quadrato si vedono 3 lati, quindi occorre aggiungere 2. Ok, gli è servito il disegno completo ma è stato bravo nella conclusione.
Aurora scrive invece
Eseguo: 37-5=32. 37 sono i quadrati tot., 5 i quadrati già disposti. Adesso devo fare 32*2=64+12=76 cm, Eseguo 32*2 perché ogni volta che aggiungo un quadrato aggiungo 2 lati (da 1 cm) al perimetro di 12 cm dei quadrati già disposti.
Più di uno ha così ragionato
La disposizione a scala, negli estremi ha sempre un quadrato di cui restano scoperti 3 lati, mentre gli altri quadrati hanno solo 2 lati scoperti. Quindi dai 37 quadrati tolgo il primo e l'ultimo e ne restano 35. Moltiplico per 2, che sono i lati utili per calcolare il perimetro e ottengo 70. Poi sommo i lati dei due quadrati tolti inizialmente, 3 lati * 2 quadrati, ottengo 6 che sommo ai 70. Il perimetro della scala di 37 quadrati con lato di cm 1, sarà di 76 cm.
Paola scrive
Per trovare il perimetro di 37 quadratini disposti a scala, conto per ogni quadratino 2 lati (da 1 cm) e li moltiplico per 37: 2*37 = 74 cm. Però nel primo e nell'ultimo quadratino conto un lato in più = 1+1 = 2 cm. Quindi faccio: 74+2 = 76 cm.
Il ragionamento di Paola e di Yuri, rispondono dunque alla domanda proposta dal prof. Davide per puntare più in alto: qual è il perimetro della figura di n quadratini?
Raccogliendo in un’unica formula il ragionamento di Paola: 2*37+2, se il numero di quadratini fosse n (n è un numero naturale qualsiasi), scriveremmo: 2*n+2. Ma Paoletta non lo ha fatto
Poi la soluzione inviata da Maria
Risposta: il perimetro è di 76 centimetri
Procedimento: ho seguito il consiglio che ha dato la professoressa, mi son fatta la colonna con il numero dei quadratini e il perimetro nell’altra colonna. Mi sono fermata a 5 quadratini, così:
1 4 cm
2 6 cm
3 8 cm
4 10 cm
5 12 cm
Mi sono accorta che ad ogni quadratino aggiunto il perimetro aumentava di 2 cm, allora ho fatto 37 per 2 ottenendo 74. Ho fatto poi 74+2 perché moltiplicando per due toglievo due centimetri al primo e all’ultimo quadratino. Infine ottengo 76.
Chiaramente Maria da una spiegazione non propriamente algebrica, non vede la regolarità, la legge che lega valori numerici corrispondenti (non era semplice per i ragazzi della classe prima, ho suggerito la tabella come primo approccio per studiare regolarità, lo abbiamo fatto in classe...), comunque è corretta la sua intuizione.
Infine la soluzione di Roberta
(la quale -anche altri risolvono ma lei mi invia la risposta via e mail- risponde anche alla mia provocazione, rivolta alla classe dopo aver visto il disegno dell’intera scala da 37 quadrati: e se la scala fosse formata da 1271 quadrati? eh... non l’avrei disegnata tutta)
Roberta segue il ragionamento visto sopra, fatto da più di uno dei ragazzi: 35 quadrati hanno due lati non in comune con quelli adiacenti quindi utili per il perimetro, mentre 2 quadrati hanno tre lati non in comune con altri. Perciò il calcolo: 35*2 +6.
Secondo tale ragionamento, Roberta scrive la formula matematica valida per n quadrati, in questo modo:
(n-2)*(2*1)+6
(2*1) perché ogni lato è lungo 1 cm
Tutti insieme ci siamo poi divertiti a semplificare la sua formula:
eseguito 2*1 che è uguale a 2 (!),
la formula diventa: (n-2)*2+6
Applichiamo la proprietà distributiva della moltiplicazione (il fattore 2 distribuito a minuendo e sottraendo) e otteniamo:
2*n –4 +6
ma -4+6 = +2 (risolto dai ragazzi eh!)
Ecco dunque la formula semplificata: 2*n+2
E’ quella di Yuri (e Paola)!
Bene, ora le risposte della terza inviate da: Alessia, Elisa, Gian Franco, Antonella, Miriam, Giuseppe P.
Miriam e Giuseppe, seguono il ragionamento visto sopra (Roberta &...). Miriam utilizza le due formule (indica con l la misura del lato del quadrato):
(35 x 2l) + (2 x 3l) = 70 + 6 = 76 cm
Lo stesso concetto si può esprimere tramite un'altra formula: (37 x 2) + 2l = 74 + 2 = 76
In quest'ultima formula, a differenza dell'altra, il lato esposto che, sia il primo che l'ultimo scalino hanno in più (rispetto agli altri 35), viene sommato singolarmente dopo. Infatti, prima si moltiplicano tutti i gradini per due, come se tutti avessero due lati esposti (37 x 2) e poi si sommano i due lati al risultato precedentemente ottenuto.
Risposta alla seconda domanda: la formula generale è: 2n + 2
Alessia e Gian Franco risolvono entrambi utilizzando linguaggi più specifici. Gian Franco:
Ho cercato di trovare una regolarità. Mi sono preparato una tabella di valori esprimendo il perimetro in funzione del n° dei quadrati:
x (n°quadrati) y (perimetro)
1 4 cm
2 6 cm
3 8 cm
4 10 cm
5 12 cm
37 ?
Osservando questa tabella ho notato che y è sempre il doppio di x + 2. Così ho potuto trovare una formula generale: 2n+2. Il perimetro della figura con 37 quadrati è 2*37+2=76 cm
Poiché Gian Franco ha parlato di funzione, la prof gli chiede la y = f(x). Risponde, risponde... : “la funzione è y=2x+2, cioè p=2n+2” Mi aggiunge: “cioè una retta che passa per il punto 2 dell'ordinata” [ah, questi raga mi fanno penare ma mi danno anche qualche soddisfazione!]
Alessia:
Per prima cosa mi sono fatta una tabella dei valori per capire la regolarità del quesito:
n quadrati | P (cm)
_______________
1 | 4
2 | 6
3 | 8
4 | 10
5 | 12
n | 2n+2
Dalla tabella noto che: aumentando di una unità il numero di quadrati, aumenta di 2 unità il perimetro, noto che il perimetro è sempre maggiore di 2 del doppio del numero di quadrati.
Quindi calcolo il perimetro dal numero n di quadrati: P=2n+2
Quindi, il perimetro della figura di 37 quadratini è 2*37+2=76u
Anche Elisa e Antonella (quest’ultima con tabella) arrivano alla legge per trovare il perimetro. La legge è quindi: 2n+ 2, intendendo come n il numero dei lati.
Quesito 3 l’area colorata
Per la prima risolvono correttamente: Paola, Aurora, Roberta, Yuri, Andrea, Maria, Luca, Antonio, Marta C.
Per la terza: Alessia, Elisa, Gian Franco, Antonella, Miriam, Giuseppe P.
Le soluzioni fornite da entrambe le classi possono riassumersi nei due tipi (immagini dalle soluzioni):
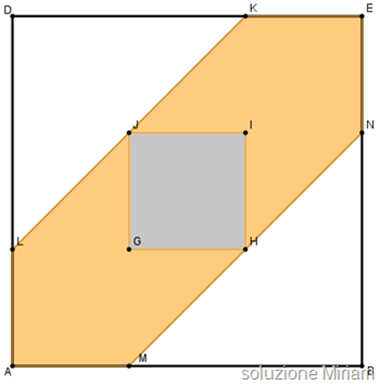
Miriam, come altri che risolvono alla stessa maniera, così spiega:
Per trovare l'area della parte colorata in arancione ho pensato di sottrarre dall'area del quadrato bianco (ABED), l'area del quadrato grigio (GHIJ) e gli equivalenti triangoli (DKL e BMN)
Mi sono calcolata le aree dei poligoni suddetti:
-Quadrato ABED, Area= l x l = 3 x 3 = 9 cm^2
-Quadrato GHIJ, Area = l x l = 1 cm^2
-Triangoli DKL e BMN, rettangoli
La misura dei due cateti è 2/3 del lato del quadrato bianco, quindi 2 cm. Quindi: Area = (b x h) : 2 = (2 x 2) : 2 = 2 cm^2 (per ciascun triangolo)
Quindi, ho fatto la sottrazione:
Area parte arancione = 9 cm^2 – 1 cm^2 - 4 cm^2 = 4 cm^2
Scrivono molto bene le soluzioni anche Andrea, Roberta, Antonio, Giuseppe e Luca (ma Luca avrebbe dovuto costruire la figura).
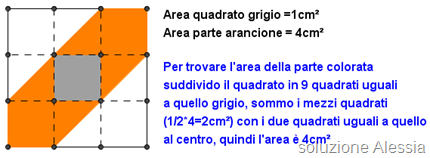
Yuri dice:
L'area della porzione arancione è di 4 cmq.
Sono arrivato alla soluzione disegnandomi su un foglio di carta il quadrato presente sul web. Nella parte arancione ho tracciato otto triangoli rettangoli con lato 1 cm (di conseguenza due di questi triangoli formano un quadrato esattamente uguale a quello grigio). Quindi mi sono calcolato l'area di questi 4 quadrati e sono arrivato a 4 cmq.
Soluzione di Gian Franco:
Oh, è fatta anche stavolta. Solite lodi a chi ha lavorato, lodi speciali a chi non ha mollato dopo le osservazioni della prof, pure provando un attimo di scoramento, e anche a chi si è deciso a partecipare ai giochi
Grazie come sempre al prof Davide e ...
vado a controllare se ha pubblicato il suo post-soluzioni ...
Sì, vedo che io sono più ritardataria!
Leggerò tutto, fatelo anche voi, per ora ho intravisto la sua conclusione e comunico: decido di regalare i nuovi giochi per le vacanze di Natale (oh, così avete un sacco di tempo per le soluzioni!)
A prestissimo dunque!




























Eh sì, a volte qualche soddisfazione arriva.
RispondiEliminaQui vedo alcune cose proprio belle. La semplificazione della formula, la retta di Gianfranco... un po' come dei piccoli regali di Natale per la prof!
Anche stavolta faccio i miei complimenti a tutti. In più aggiungo un pacchetto di auguri per le vacanze di Natale! (Qui ci starebbe bene una musichetta tipo Jingle Bells di sottofondo.)
E naturalmente aspettiamo tutti i nuovi giochi in dono :-)
:-)) ... arrivano fra un po'
RispondiEliminaGrazie a nome di tutti. Già già, piccoli regali. Insieme alle due verifiche da correggere ... noi fatte.
Grazie per gli auguri natalizi che ricambiamo. Stamane ci siamo concessi di donare l'ora alla prof di musica per ascoltare le musichette in vista del saggio per Natale. Jingle compreso :-)