Ecco le nostre soluzioni del
Sarà mica matematica 34 del prof Davide.
Quesito 1, somma di numeri consecutivi
Come accennato nel post di presentazione dei quesiti, mi aspettavo cose ...
Poiché in classe, in entrambe le classi, è già capitato di generalizzare per esprimere numeri consecutivi, precedenti, quadrati, ecc... Purtroppo non sempre si riesce a utilizzare informazioni. Forse perché si chiedeva di sommare e allora... si è resa necessaria qualche tiratina d’orecchie, diciamo così.
Hanno risposto per la classe seconda: Antonella, Alessia, Gian Franco, Miriam, Elisa.
Quasi tutti hanno provato in un primo momento a sommare tre numeri consecutivi a piacere e notato che la somma è sempre divisibile per 3. Anzi qualcuno dice che il risultato è sempre uguale al numero centrale moltiplicato x 3.
Certo, certo, è così. Poi lo dimostreremo con la formula trovata da voi ... dopo la sollecitazione a considerare con attenzione i numeri consecutivi e esprimerli generalizzando!
Infatti, sintetizzando le varie risposte, siete arrivati a dire:
ho preso diversi casi di tre numeri consecutivi (un consecutivo di un numero si ottiene aggiungendo 1 al numero stesso. Detto in modo generico i numeri sarebbero n, n+1, n+2, n+3...ecc...) ad esempio: 10 11 12; 34 35 36; 41 42 43.
Allora provo a generalizzare, cioè sostituisco il primo addendo con la lettera "n", quindi ho:
n+(n+1)+(n+2)
è la formula generale per sommare tre numeri consecutivi. Ma poi, guardandola meglio in faccia [] ho fatto un aggiustamento che la rendeva più fluida e semplice:
Dopo ho fatto la prova per sicurezza con un numero qualsiasi e funzionava!
La formula funziona anche se c'è lo zero perché se si ipotizza che lo zero sia n è come fare 0+1+2 oppure 3*0+3: ottengo sempre 3.
Per trovare la formula del calcolo di 4 numeri consecutivi ragiono come per la precedente ma la formula risulta così:
n+(n+1)+(n+2)+(n+3)= 4n+6
perché prima sommo le "n" (n+n+n+n=4n) poi sommo i numeri specifici (1+2+3=6).
Queste due formule sono valide se è presente lo zero tra gli addendi e anche se gli addendi sono numeri negativi.
Ahah, ma mica dimostrate che siano valide per i numeri negativi. Sì, qualcuno somma, e anche correttamente, dei numeri negativi consecutivi:
(-5)+(-4)+(-3) = –12; (-6)+(-5)+(-4)+(-3) = –18
ma non dimostra come le formule siano valide. Ma, va bene su, siete in seconda!
Ora invece dimostriamo perché la somma di tre numeri consecutivi sia un multiplo di 3. Osservate la formula trovata:
3n+3
Non è il triplo di un numero a cui si aggiunge ancora 3? Perciò non può che essere un multiplo di 3.
E poi, perché tale somma è sempre uguale al numero centrale moltiplicato x 3 ?
3n+3 possiamo anche scriverlo così:
3 *(n+1)
Sarebbe come sfruttare la proprietà distributiva al contrario, no? Se dobbiamo eseguire 3*(n+1), applicando la distributiva otteniamo: 3n +3. Ok?
Ma nella sequenza di tre consecutivi qualsiasi, (n-1) non è il numero centrale? Ecco: 3*(n+1) è il numero centrale moltiplicato per 3!
Passiamo ai solutori, sempre in numero inferiore, della classe terza. Ebbene sì, l’assenza di voglia di fare è sempre più dichiarata. Ok, va bene tutto, costringere non è piacevole né utile e poi si può fino a un certo punto. Seppure con l’intervento dei genitori. Ma se non nasce qualcosa dentro, se non si prova una qualche spinta, se non si prova alcun piacere a mettersi in gioco, se, se ... lavorare solo per costrizione non porta a nessuna crescita. Fate voi!
Il quesito è risolto da: Manuel, Pietro P. e Gabriele G.
Loro ovviamente, basta un minimo di volontà, se la cavano meglio con l’astrazione e con il calcolo con i relativi.
Manuel scrive:
La formula per rappresentare la somma di tre numeri consecutivi è:
n+n+1+n+2=3n+3.
Ho indicato con n un numero naturale qualsiasi e di conseguenza ho indicato con n+1 il consecutivo e con n+2 il secondo numero consecutivo.
Se i numeri sono negativi questa formula vale lo stesso per esempio:
-4-3-2=-9; applicando la formula: -4*3 +3=-12+3= -9
Questa formula vale anche per lo 0, per esempio:
0+1+2=3; 3*0+3=0+3=3.
La formula per rappresentare 4 numeri consecutivi è:
n+n+1+n+2+n+3= 4n+6.
Gabriele scrive:
dopo aver fatto alcuni tentativi ho capito che la somma di tre numeri consecutivi qualsiasi è sempre divisibile per tre, perché è come moltiplicare lo stesso numero per 3 e aggiungere 3, come riportato nell’esempio:
2 + 3 + 4 =
=2 +(2+1)+(2+2)=
=2+2+2+1+2=
=2*3+3
Che generalizzata sarebbe
a +(a+1)+(a+2) =
=a + a + a + 1 + 2=
=3a+3
E basta.
Pietro:
la formula è: a+(a+1)+(a+2)=3a+3
a è un numero qualsiasi, a+1 è il successivo, a+2 il successivo di a+1.
Per i numeri negativi: se a=-2, a+1=-1 e a+2=0
la somma sarà: (-2)+(-1)+0=-3
applichiamo la formula: -2*3+3=-6+3=-3
Per sommare quattro numeri consecutivi: a+(a+1)+(a+2)+(a+3)=4a+6
Quesito 2, somma di numeri ai vertici di un cubo...
Risolvono per la seconda: Antonella, Alessia, Gian Franco, Miriam, Elisa, Erika e Mattia.
La soluzione è la seguente:
Altre soluzioni, disponendo i numeri in vertici diversi, sono equivalenti.
Copio la spiegazione di Gian Franco che è la più completa.
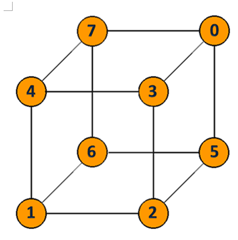
Prima di tutto mi sono scritto i numeri da 0 a 7 che a mano a mano ho segnato, e i numeri primi che potevo ottenere sommando i numeri dati. Ho pensato di iniziare posizionando lo 0 in un casella qualunque. A questo ho collegato tutti i numeri dispari tranne l'1 perché 0+1=1 non è un numero primo. Tra il 5 e il 3 c'era un vertice vuoto quindi lì ho posizionato il 2 che non potevo collegare al sette.
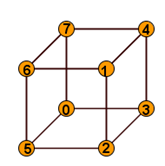
Poi ho guardato i numeri che mi erano rimasti, ho preso l'1 e l'ho posizionato sopra il 2, - la soluzione di Gian Franco è questa:
il 4 l'ho posizionato sopra il 3 e il 6 l'ho posizionato sopra il 5. Questi ultimi passaggi li ho fatti naturalmente in modo tale
da formare numeri primi.
Ho così ottenuto più numeri primi uguali, questo era scontato perché il numero primo più alto che si può ottenere è il 13, cioè la somma dei numeri più grandi a disposizione (6+7), poi da 0 a 13 ci sono 6 numeri primi e gli spigoli del cubo sono 12, quindi era impossibile che ci fosse un numero primo per ogni spigolo.
Per la terza risolvono... niente di meno che: Pietro P. e Bachisio in maniera esatta. Pietro al secondo tentativo perché, come Manuel e Gabriele G., che invece non si sono presi la briga di un secondo tentativo, direi che aveva letto le indicazioni a dir poco sbrigativamente!
Le spiegazioni di Pietro e Bachisio... ah, il loro italiano è piuttosto faticoso da leggere. Rinuncio!
Bene, mi pare di aver concluso. Bravo a coloro che si sono impegnati, buon per loro!
Grazie come sempre al prof Davide.
I prossimi giochi, finite le vacanze pasquali.
Buona Pasqua a tutti!

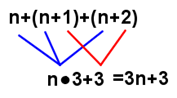
























Accidenti, comincio ad essere in ritardo anche nel commentare!
RispondiEliminaChe dire? Posso solo associarmi alle parole della prof: complimenti a tutti quelli che si sono impegnati di persona personalmente. Non solo ne avranno sicuro giovamento ma sono anche riusciti a trovare delle belle risposte!
Alla prossima!
Grazie, prof.
RispondiEliminaVedi come si è tranquilli da queste parti.... niente folla.... :-(
Be', la tranquillità ha i suoi vantaggi :-)
RispondiEliminaPossiamo dire pochi ma buoni?
A me pare che, per parafrasare Shakespeare, c'è del buono in Sardegna :-D
Che poi non è che dalla mie parti ci sia una vera folla. Un finta folla, diciamo così.
Sì sì, siamo ottimisti: assieme al marcio c'è anche del buono :-)
RispondiEliminaGrazie per l'incoraggiamento!