Ecco le nostre soluzioni del
Sarà mica matematica 32
Voglia di lavorare (e di migliorarsi) saltami addosso per alcuni... senza far nomi, ma tant’è!
Hanno risolto il
Quesito 1, riempire il quadrato di sedici caselle....
Per la seconda: Miriam, Alessia, Antonella, Arianna, Elisa, Gian Franco, Erika, Giuseppe P.
Per la terza: Pierluigi, Manuel, Gabriele G., Pietro P., Bachisio
La soluzione:
Quasi tutti i solutori, qualcuno ha inviato solo la soluzione, scrivono di aver capito che “occorreva mettere più volte possibili il numero 4 (o le cifre maggiori) nella parte arancione, perché avendo meno caselle disponibili, servivano cifre più grandi per arrivare a una somma che potesse essere uguale alla somma nella parte bianca.”
Gian Franco dice, più ampiamente:
Innanzitutto, ho osservato la figura per bene e, siccome ogni riga e colonna doveva essere formata da 1, 2, 3, 4, sommandoli si ottiene 10 e moltiplicando questo per 4 cioè per il numero di righe o colonne si ottiene 40 che diviso fra le due parti fa 20, cioè la somma di ogni parte doveva essere 20. Quindi, siccome la parte arancione è più piccola di quella bianca, in quella colorata ci dovevano essere le cifre maggiori.
Allora ho cercato di ottenere 20 nella parte colorata usando soprattutto 4, 3, 2. Ho messo tre 4 in diagonale per non ripetersi in verticale, la stessa cosa ho fatto con i due 3 e infine ho messo il 2 perché rimaneva solo uno spazio. Poi nella parte bianca ho completato le caselle in modo da non far ripetere i numeri e ho ottenuto il risultato.
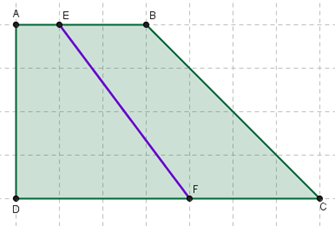
Quesito 2, suddivisione trapezio in due parti equivalenti
Per la seconda risolvono: Alessia, Miriam, Antonella, Gian Franco, Giuseppe P., Elisa. Erika ha provato ma non giunge alla soluzione esatta. Brava comunque.
I numerosi solutori della terza sono: Pierluigi, Marco, Manuel, Gabriele G.
La soluzione:
Il ragionamento dei ragazzi della seconda, ricalcano il seguente (il solito Gian Franco che non lesina esplicite spiegazioni):
Ho prima calcolato l' area del trapezio ABCD usando la formula: (B+b)x h : 2 e ho ottenuto 20 [quadratini, riferendoci alla figura del quesito]. Siccome le due figure da ottenere tracciando il segmento EF dovevano essere equivalenti, ho diviso 20 per 2 cioè 10. Così dopo aver riflettuto sono arrivato alla decisione su come tracciare il segmento.
Ho notato che tracciandolo avrei ottenuto due trapezi quindi ho provato a trovare un'area che fosse uguale a 10.
Siccome la base minore del trapezio a sinistra era di 1 e l'altezza di 4, per ottenere l' area stabilita dovevo contare 4 nella base maggiore per ottenere 5 nella somma della basi, che moltiplicato per 4 e poi diviso per 2 mi dava 10. Infine per essere sicuro di aver tracciato bene, ho calcolato l'area dell'altro trapezio e ho ottenuto lo stesso risultato. ---Formule:
Giuseppe P. disegna con l’aiuto di babbo, la figura seguente, che lascia intendere il ragionamento:
Bravo, Giu’!
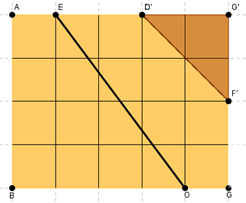
Manuel risolve così:
Ho costruito un rettangolo 3*4 (EFGH), successivamente ho tracciato la diagonale EG (così facendo ho diviso il rettangolo in due parti uguali).

Facendo il conteggio dei quadrati si può vedere che la diagonale divide anche il trapezio in due parti equivalenti perché:
- la parte sinistra è formata da 4 quadrati + metà rettangolo;
- la parte destra è formata da 4,5 quadrati + metà rettangolo - 0,5 quadrati (la parte aggiunta per poter formare il rettangolo), cioè è formata da 4 quadrati in tutto + metà rettangolo.
Quindi l'area a sinistra e a destra del segmento EG sono equivalenti.
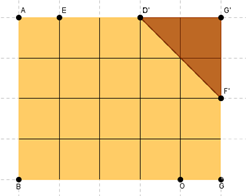
Gabriele G., ragiona così:
Osservando il trapezio ho provato a trasformarlo in unrettangolo equivalente per riuscire con più facilità a dividere a metà la figura. Ho segnato il punto medio del segmento DC che ho chiamato F, poi un punto, G, per formare il triangolo rettangolo FCG .
questo l'ho ruotato di 180° attorno a F, in senso antiorario ottenendo così un rettangolo
di base 5 e altezza 4, equivalente la trapezio iniziale. A questo punto, facilitato dai quadratini, ho capito che segnando sulla base BG il punto O, unendolo poi al punto E, ottengo due figure equivalenti (due trapezi equivalenti) come richiesto dal problema.
Bene, detto tutto? Mi pare di sì. Non mi resta che il
solito BRAVO a chi lavora,
Grazie al prof. Davide.
L’appuntamento a breve (domani pomeriggio?) qui, per i nuovi quesiti.





























Perbacco! Belle risposte, devo dire! Soprattutto per il secondo quesito avete trovato un paio di soluzioni molto originali e creative. Bravi! Peccato per quelli che non si sono fatti saltare addosso dalla voglia di lavorare...
RispondiEliminaL'altra considerazione che posso fare è... sono ancora una volta in ritardo! Però conto di pubblicare le nostre soluzioni entro sera. Poi aspetterò con ansia i nuovi giochi :-)
Grazie, prof. A nome di quelli che lavorano! :-)
RispondiEliminaIo stavolta mi sono letteralmente imposta di pubblicare per non rischiare un ritardo mostruoso....
In compenso posso rinviare i nuovi :-) :-) NO, non troppo, domani!