Video estate_2

Ragazzi,

ancora vostre creazioni. Stavolta è Marco D che accompagna Beatrice.

Bravi! Al prox video?

Estate: fantasia e colore! Video

Ragazzi,

I vostri lavori estivi, con fantasia, cominciano ad arrivare!

Ho deciso di metterli in un (primo ?) video. Per ora ci sono solo Davide D. e tanta Beatrice!

Vedete!

Ho scordato di mettere il Fiore di Bea. Aggiungo qui l’applet:

Per fare un fiore ...

ci vuole un quadrato!

 Clic

Se volete costruirlo anche voi, scaricate Scheda_4 Fiore.pdf.

Il quadrato dunque, magico come qui, e ancora:

un quadrato ruota dentro un altro quadrato e i segmenti-lato generano curve! - Ah, è un fenomeno che conosciamo già, lo so... Ma la segnalazione del prooof mi è piaciuta! - Fate clic

Perché ogni scarabocchio ...

“è figlio di mamma Matematica”! 

Raga,

vi ho ricordato da poco l’affermazione fatta da un matematico, che, più o meno, suona così. Tant’è che ...

Di recente, nel corso di una riunione, mentre ascoltavo, come al solito scarabocchiavo. E fra i miei scarabocchi mi sono ritrovata un bel simbolo dell’infinito! Lo conoscete: ∞

Mi sono chiesta poi: ma ci sarà, quale sarà, la legge matematica che rende conto di questo simbolo? Cioè quella che si dice, in matematico, la sua equazione.

E certo, c’è! Non la sapevo ma non è stato difficile trovarla!

La seguente. E’ un po’ complicata per noi, ma è bello sapere:

(x²+y²)² = 2 a² (x² - y²)

E ... Geogebra mi disegnerà questo simbolo, o meglio, questa curva?

Come no! Sul campo di inserimento di Geogebra ho dovuto digitare così:

Curva[a sqrt(cos(2 α)) cos(α), a sqrt(cos(2 α)) sin(α), α, 0, 2 pi]

Bella no?

Oh, non spaventatevi, fra qualche anno appena, queste cose le saprete più di me! (ricordate? ve lo dico sempre!)

La curva matematica a forma di infinito ha un nome. Si chiama Lemniscata di Bernoulli.

Fu descritta per la prima volta nel 1694 da Jakob Bernoulli, un matematico e scienziato svizzero, dal quale prende il nome.  Bernoulli la chiamò lemniscus, che in latino significa ‘nastro annodato’: nell’antica Roma era un nastro pendente dalle corone.

Ed ecco il risultato con Geogebra. Clic! – Potete animare o muovere lo slider.

Maa...

più bello è vederla formarsi da una circonferenza come luogo!

Iperbole e circonferenza

• Si costruisce un’iperbole equilatera (in seconda sanno già l’equazione: x * y = k oppure y = k/x)
• poi una circonferenza di centro A, un punto dell’iperbole,
• passante per il centro dell'iperbole

Il luogo delle circonferenze al variare di A è una lemniscata di Bernoulli.

Guardate un po’. Cliic!

E non finisce qui. Si può costruire la lemniscata anche come luogo di punti. Lo vedete su un’altra applet. Clic

E con la simmetria?

Eh eh ... giocare, giocare!

Questo l’ho fatto io!

O così?

Ma ovvio che ho giocato ispirandomi a QUESTI BEI LAVORI!

Andate a vedere tutti i lavori di gruppo!

Ragazzi, ringraziando sempre maestra Renata, vi dico

 Come si fa. Ma, si lavora di fantasia!

- Prima dovrete aver imparato i giochi precedenti.

- Dovete poi costruire i simmetrici di determinati punti rispetto a due rette perpendicolari (basta anche rispetto agli assi cartesiani – visualizza Assi, su Geogebra –)

- Come esempio controllate l’applet della mia costruzione, su cui lascio visualizzati tutti gli oggetti. I punti iniziali sono A, B, D, E, gli altri sono ottenuti da rotazione e simmetria.

Sull’applet trovate altre indicazioni.

A voi personalizzare! - Compreso l’intervallo dello slider, il suo incremento e la velocità.

Potete anche scaricare il file con il doppio clic e salvare. Ora clic su img.

Buone costruzioni!

Forme, colori, fantasia!

Ragazzi,

giocando con geogebra!

Guardate l’immagine: sono lavori dei ragazzini di Maestra Renata. Allora. Oggi ragazzi, giusto della vostra età (dico agli ex-prima!)

Realizzati facendo ruotare dei punti sul piano. Fate clic sull’immagine per vedere l’animazione. Poi vi spiego sotto....

Visto? Volete provarci? Non è difficile!

Vero che vi piacerebbe disegnare il cuore?

-- Certo, un cuore: sappiate che si tratta sempre di curve matematiche. In seconda già abbiamo commentato una frase di un matematico, filosofo,..., la abbiamo sulla nostra sidebar:

Se segnassimo a caso dei punti su un foglio di carta, si potrebbe individuare sempre e comunque un'equazione matematica tale da rendere conto di quanto fatto. (Leibniz)

Voi conoscete già delle curve matematiche: la retta (sì, anche la retta è una curva matematica), il cerchio, l’ellisse, la parabola, l’iperbole. Tutte hanno una loro equazione. Ma questo lo impareremo più avanti...!

E il cuore è la curva matematica chiamata Cardioide, "a forma di cuore" [dal greco kardioeides: kardia (cuore) e eidos (forma)].

  Abbiamo, andate a vedere...che belle!

La cardioide e Regali ... di cuore! --

Ebbene, torniamo a giocare! Ho preparato una Scheda di lavoro che vi guiderà passo a passo. Scaricate Scheda_3 Ruota punti

 Attenzione: trovate l’elenco dei documenti in ordine alfabetico; per trovare prima il documento da scaricare, fate clic sull’intestazione: Data ultima modifica. Cliccate sul nome del documento e si aprirà immediatamente la finestra per salvare.

Leggete tutto e scatenate la fantasia! E, se.... inviate!

E a proposito di Prove Invalsi ...

Sono io la curiosa!

E sì, ragazzi, che rispondiate ora, che lo facciate come ripasso estivo ... Io so che qualcuno di voi uno sguardo sul blog continua a darlo, dunque:

sono curiosa di sapere come ve la sareste cavata con qualche quesito della Prova Invalsi d’Esame di quest’anno.

No, non importa se voi non avete fatto la terza! I quesiti sono vari, non necessariamente “da terza media”.

Dunque, ecco alcuni quesiti che mi hanno incuriosito (vale per la ex-classe I e per la ex-II!). Se necessario, cliccate per ingrandire le immagini.

1. Mi fa piacere se spiegate le vostre risposte!

2.  strafacile!

3.

4. solo per i ragazzi di II

5. io dico che risolvono anche i ragazzi di I!

6. non dico nulla, con le lettere si possono fare le operazioni ...!

7. ultima!

ciao, carissimi

Prove Invalsi 2011

i ragazzi delle classi III

hanno sostenuto oggi le Prove Nazionali Invalsi.

Noi non siamo impegnati in Esami, ma per qualche alunno delle III che eventualmente controllasse, ansiosamente , sul blog, segnalo:

Le soluzioni (e i punteggi) si possono scaricare QUI (Matematica e Italiano)

I fascicoli con i testi delle prove potete scaricarli da prof. Daniele

Ho parlato delle classi III: se qualcuno della ex-seconda è poi curioso, ben venga!

Excel e atomi

... più precisamente

Configurazione elettronica degli elementi

Il mio amico Roberto, che con Excel ci fa ... fra un po’ anche il caffè, ha realizzato ancora un bel lavoro che ci sarà utile nello studio della nostra chimica.

Ha “giocato con un grafico a dispersione per ottenere la configurazione elettronica degli elementi.
Il grafico nel file Atomi.xlsx, usa una tabella dove sono riportati gli elettroni presenti nei diversi stati energetici.”

”Nel file Elettroni_in_movimento.xlsm, ho aggiunto alcune serie che permettono di separare gli elettroni più esterni. Inoltre grazie ad una piccola macro, che semplicemente aggiorna il valore dell'angolo di rotazione e di volta in volta avvia il ricalcolo per aggiornare il grafico, si ottiene il movimento proprio di quegli elettroni esterni che sono di fatto i più instabili. Quindi un click sul pulsante Demo start attiva il movimento che può essere poi interrotto da una seconda pressione (il pulsante intanto ha cambiato caption diventando Demo stop).”

Clic sull’immagine sotto per leggere Roberto e scaricare i file

Ragazzi, per noi ho adattato il file di Roberto, Elettroni_in_movimento.xlsm, modificando la tabella degli elementi:

- ho evidenziato con una diversa formattazione, gli elementi che noi dobbiamo conoscere meglio, di cui ci interessa fissare le proprietà elettroniche.

- li troviamo in testa alla tabella secondo la valenza crescente: ordine crescente secondo i gruppi A (ci aiuta a memorizzare per gruppi di elementi, gli elettroni di legame e quali elementi si legano più facilmente tra loro, la loro "tendenza alla combinazione", la loro affinità chimica)

- in un nuovo foglio di lavoro ho inserito l’immagine della Tavola periodica degli elementi, da tenere sempre presente!

Potete scaricare

Copia di Elettroni_in_movimento.xlsm 

Grazie Roberto!

PS: Per coloro che leggono in questo periodo.

Potete giocare con il Mitico gioco Pong (i ragazzi di seconda già ci hanno giocato!), sempre di Roberto.

Sumdog, gareggia e impara!

Ragazzi,

amanti di gare e videogiochi,

vi segnalo, attraverso prof. Daniele, Sumdog,

un sito che offre decine di giochi didattici interattivi.

Si può gareggiare: dopo aver scelto e personalizzato un avatar è possibile sfidare altri studenti della propria scuola o di un altro istituto in qualche parte del mondo.

I giochi sono coloratissimi, veloci e molto apprezzati da ragazzini abituati ad usare sofisticate console di gioco.

Clic sull’immagine, dal video che illustra le principali caratteristiche del sito, leggete ancora dal prof. Daniele, collegatevi al sito e... buone gare!

Buone vacanze!

Ragazzi,

la scuola è finita!

Vi siete impegnati, non vi siete impegnati, siete stati calmi, siete stati agitati, mi avete fatto sorridere, mi avete fatto sorridere ... meno, ma siete cresciuti e avete realizzato delle belle cose!

Auguro

e ricordate di passare ogni tanto ... qui, da casa vostra!

Aggiorno, i carissimi non mi lasciano sola!

Il buone vacanze di  Beatrice. Con l’amato Geogebra!

- Mi dice di averlo già pronto da qualche giorno, non so perché non me l’abbia detto prima!

Oh, brava Bea, c’è un bel po’ di paziente lavoro!

Triangoli isosceli equivalenti

Ormai ultimi lavori dell’anno scolastico ...

Stefano, Beatrice, Davì e Davide D. hanno realizzato su Geogebra il lavoro sui triangoli isosceli equivalenti, mostrando anche qui varianti, invarianti e ... minimi!

Triangoli di Stefano. Clic su img

Beatrice ... non scorda mai la Patria! Clic

Davì e Davide, ah, siamo proprio agli sgoccioli ...: buone le costruzioni ma non curano troppo grafica e commenti!

Tuttavia: bravi tutti!

Dall’ellisse alla parabola

Davide D.

ha fatto un altro esercizio con Geogebra.

Lasciando fisso uno dei due fuochi dell’ellisse, allontaniamo il secondo fuoco lungo la retta che li contiene. Si ottengono delle ellissi sempre più “allungate”.

Immaginando il fuoco F’ che “sfugge all’infinito” , si passa dall’ellisse alla parabola.

L’esercizio evidenzia anche la proprietà dei fuochi dell’ellisse e del fuoco della parabola (Davide mostra sulla costruzione ma non scrive, lo faccio io! ).

Un raggio di luce, emesso nel fuoco F, dopo aver colpito l’ellisse in un suo punto, viene riflesso nel fuoco F’.

Passando dall’ellisse alla parabola, rimane un unico fuoco F. I raggi di luce riflessi sono ora paralleli. Come ci aveva mostrato Bea.

Clic sulla prima immagine

Bene Davide!

Con archi di parabola

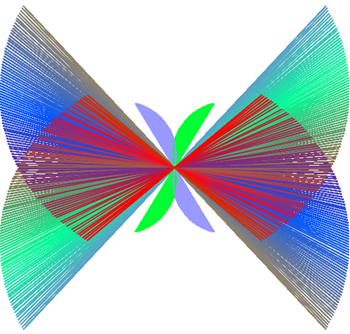
E ancora dalla parabola

come inviluppo di segmenti:

  

Ecco il Fish red-blue di Davì con Geogebra

Questo di Stefano su foglio da disegno

Per ora ho solo questi, pubblico per incoraggiare ... [per chi assente, pag.214 Es.49]. Ma pensate ad altri “quadri”!

Ecco il my pendant di Beatrice

E Bea ha perfezionato dandoci la possibilità di creare ... quante figure!!!

Io ho creato le quattro belle simmetrie qua sotto. Clic sulle prime per aprire l’applet.

Davì ha realizzato ancora la navicella spaziale!

Bravii!

Aggiungo il lavoro di Davide P. che lui chiama simbolo. Ma io non so di che! La costruzione è ben fatta. Bene, Davide!

E, fiore coloratissimo di Daniele

Bene, Danie’