Ho voluto provare
da Geogebra: “Esporta Vista grafica come Gif animata”
Con una dimostrazione del Teorema di Pitagora che ancora non avevamo.
Verifichiamo come funziona la gif...
[Aggiornamento]
La mia amica Renata mi invia la gif modificata nei tempi dei singoli fotogrammi (si può leggere nei commenti un suggerimento), così che le immagini siano opportunamente rallentate per meglio apprezzare la dimostrazione.
Grazie, Renata, sempre preziosissima.
Devo devo!
Pubblicare le poche nostre soluzioni del
Sì,sono proprio poche! Le lunghe vacanze pare l’abbiano fatta da padrone. Vediamo ...
Quesito n° 1, il reticolo dei divisori
E’ stato risolto per la classe prima, da: Alessia, Gian Franco, Miriam e Giuseppe P.
Alessia, una soluzione
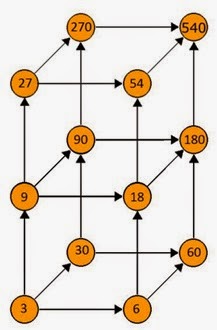
Gian Franco, due soluzioni. Dice di aver lavorato al “doppio cubo” dei divisori, usando dapprima tre dei divisori più grandi del 540, poi il M.C.D. tra due numeri (o tre).
Giuseppe P. due soluzioni, ha usato il numero 1:
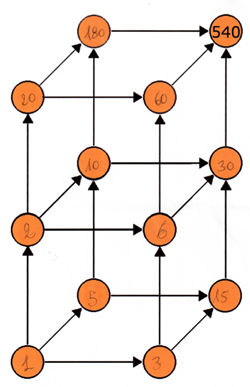
Miriam, una soluzione, e ha usato il numero 1:
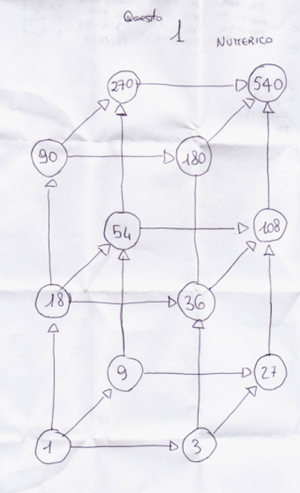
Miriam specifica le divisioni eseguite:
540:2=270; 540:3=180; 540:5=108; 270:3=90; 180:2=90; 270:5=54; 108:2=54; 180:5=36; 108:3=36; 90:5=18; 54:3=18; 36:2=18; 54:6=9; 108:4=27; 18:18=1; 27:3=9; 27:9=3; 9:9=1; 3:3=1
Per la classe seconda hanno risolto: Manuel, Pierluigi e Bachisio
Manuel, una soluzione:
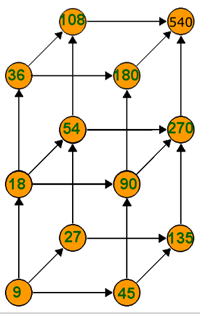
Spiega Manuel: ho diviso il 540 per i primi tre numeri primi; poi ho cercato il massimo comun divisore tra 270 e 108 che è 54, tra 108 e 180 che è 36, tra 180 e 270 che è 90; poi ho cercato il massimo comun divisore tra 36, 54 e 90 che è 18; ho trovato un divisore di 270 dividendo per 2, il 135; poi il massimo comun divisore tra 135 e 54 che è 27; successivamente ho cercato il massimo comun divisore tra 135 e 90 che è 45; infine ho cercato il massimo comun divisore tra 18, 27 e 45 che è 9.
Soluzione di Pierluigi, che usa il numero 1. Scrive di aver trovato tutti i divisori di 540 posizionandoli opportunamente nei cerchietti fino a completare il reticolo:
La soluzione di Bachisio è fornita via ‘’foglietto’’ e ... e. (punto). Non utilizza il numero 1 comunque
Quesito n° 2, la geometria, ahi la geometria!
È doveroso dire che in prima ho dovuto dare qualche dritta: quanti triangoli vedete in figura? E sono stati bravi ad individuare diversi triangoli (8 triangoli in tutto). Ancora ho suggerito che un’area può essere trovata anche per somma e/o differenza di aree...
Hanno risolto: Alessia, Miriam, Gian Franco e Giuseppe P.
Intanto vediamo l’immagine del quesito, completa degli elementi risolutivi
Alessia, ha individuato sì, fra i diversi triangoli, quelli giusti per la soluzione, cioè, il triangolo ABD, quello AOD, e il triangolo ACD. Ha necessitato però di qualche sollecitazione su come si traccia l’altezza di un triangolo ottusangolo? Ha cercato e trovato! “Bisogna prolungare la base e tracciare la retta perpendicolare alla base” Bene, così si fa e si impara!
Miriam e Gian Franco invece hanno ricordato che già in occasione di un altro quesito dei nostri giochi, gli avevo mostrato l’altezza di un triangolo ottusangolo.
Giuseppe ha risolto con l’aiuto dei genitori. Lodevole sempre il suo impegno nel rispondere alle attività proposte.
Sintetizzo la spiegazioni della soluzione del problema, dalle e-mail inviatemi dai ragazzi:
Inizialmente calcolo l' area del triangolo bianco AOD, la cui altezza è 3 cm e la base 4 cm, quindi l' area: 3*4:2= 6 cm^2. Poi traccio l'altezza del triangolo ABD, ottusangolo, che è di 6 cm; la trovo prolungando la base e tracciando la perpendicolare passante per il vertice B. Quindi l'area del triangolo ABD è 12 cm^2. Da questa sottraggo l’area del triangolo bianco AOD e trovo l'area del triangolo colorato AOB, cioè 6 cm^2. Trovo poi l’area del triangolo ACD, formato dal triangolo bianco AOD più quello colorato DOC, la cui altezza è 5 cm e la base 4 cm. Quindi l'area è 10 cm^2. Sottraggo l’area di AOD e trovo 4 cm^2, l’area di DOC. Poi sommo le aree dei triangoli colorati, AOB e DOC, e trovo l'area totale cioè 10 cm^2.
Classe seconda.
In questa classe non ritenevo opportuna alcuna dritta e: vacanze pasquali esageratamente prolungate praticamente fino al 2 maggio, arrivata nessuna soluzione!
E allora, coraggio, via con le dritte anche per loro, rinviata ancora la pubblicazione delle soluzioni. Ma, ma... l’impegno probabilmente era eccessivo, si poteva sudare e, con il cattivo tempo che qui da noi non ci vuole abbandonare, si rischiava un brutto raffreddore nel precipitarsi poi all'aria aperta a giocare!
Fine della cronaca!
Non mi resta che dire un bel Bravi ai ragazzi della prima che si sono impegnati.
Grazie come sempre al prof Davide per gli interessanti quesiti e, arrivederci al prossimo anno con i Sarà Mica e i Due a settimana... Con la speranza, no, non bisogna perderla, che i ragazzi acquisiscano la consapevolezza delle occasioni di crescita loro proposte.
Post
Tutti i commenti
