Immagino che
qualcuno di voi abbia già visto. Visto la ‘sorpresa’?
Per chi non ha letto e per chi passa di qui,
dal prof Davide i nuovi quesiti del
Carinissimi come sempre, vai con i divisori:
O, cara classe prima, se non siamo bravi con questo... eeh?? Ma anche cara seconda!
Poi c’è il quesito geometrico... Clic su immagine o sul link sopra e via a leggere le indicazioni!
Buone soluzioni (con spiegazione)!
Sì, ragazzi,
la ricordiamo tutti i giorni, l'avevamo ricordata a Dicembre per il suo 100esimo compleanno.
Emma Castelnuovo ieri è scomparsa.
Leggo, morta nel sonno...
Noi, continuerà ad accompagnarci nelle nostre esplorazioni della matematica, nelle nostre scoperte, nei nostri apprendimenti.
Come ha fatto da sempre per la vostra prof. Che deve alla grande Maestra l’amore per il suo lavoro. Le deve tutto dunque!
Ciao, Maestra, Grazie!
Link:
Come ho imparato matematica alla Scuola Media
Emma Castelnuovo: quali materiali possono usare gli studenti di geometria? (video)
Emma Castelnuovo: come imparare la geometria? (video)
Ci siamo accorti,
o meglio, mi hanno fatto notare gli alunni, l’altro ieri che nel post dei quesiti mancava la scadenza. Sono stata giustificata “perché cadeva la connessione”
E comunque, due settimane sono passate ed è l’ora delle soluzioni.
Le soluzioni, ehm ...
E’ pur vero che sostengo la relatività del concetto di facile e difficile, ma stavolta forse è il caso di ammettere che il primo quesito non era proprio facile. Se non altro alla luce delle difficoltà incontrate soprattutto dai ragazzi della classe prima. Che, seppure i soliti solutori, si sono impegnati in ogni modo per trovare la soluzione. Per quanto riguarda la seconda, non so, io continuo a pensare che manchi un po’ l’impegno necessario...
Ricordiamo il quesito 1:
Si chiedeva il perimetro di ciascuno dei triangoli che, accostati, vanno a formare le due figure, sapendo che il perimetro del parallelogramma supera quello del triangolo di 3 cm e quello del rombo lo supera di 7 cm.
Per ciò che riguarda la prima parte, possiamo dire che Miriam, Gian Franco, Alessia, Daniele e Giuseppe P. (I) hanno, chi riuscendo ad esprimersi con chiarezza, chi meno, così ragionato:
Confrontando il parallelogramma con il triangolo si nota che (indicando con l il lato obliquo del triangolo e con b la base):
le "l" ci sono due volte, sia nel triangolo che nel parallelogramma.
la "b" è presente nel triangolo una sola volta e nel parallelogramma due volte.
La loro differenza è quindi che il parallelogramma ha un lato, "b", che il triangolo non ha e corrisponde ai 3 cm in più rispetto al perimetro del triangolo.
La base del triangolo misura quindi 3 cm.
La seconda parte è quella rivelatasi difficile. E allora Miriam, Alessia, Daniele e Giuseppe hanno chiesto l’aiuto dei ‘’grandi’’. I quali hanno dato loro, che forse hanno anche capito (copio la spiegazione di Miriam), una soluzione algebrica del tipo:
Il perimetro del rombo è di 7 cm più grande di quello del triangolo quindi posso fare [impostare] un’uguaglianza:
2l+b+7 = 4l sappiamo che "b"corrisponde a 3
(Se il perimetro del rombo è 4l e il perimetro del triangolo è 2l+3 per fare l'uguaglianza devo aggiungere 7 cm al perimetro minore)
Per rendere più facile la risoluzione 2l+3+7 diventa 2l+10
Ho scoperto che "l" misura 5 cm, facendo:
il perimetro del rombo tutto intero è 4l, 2l le ho già nel triangolo quindi mi resta 10.
Gli altri 2 lati, 2l, misurano 10 e quindi faccio 10:2 = 5 ecco perché ciascun lato "l" misura 5 cm.
Quindi "b’’ misura 3 cm, "l" misura 5 cm e perciò il perimetro del parallelogramma è di 16 cm, quello del rombo è 20 cm e quello del triangolo è 13 cm.
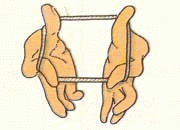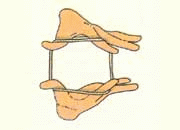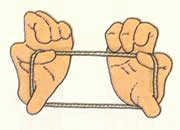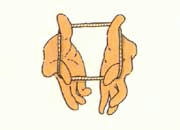
Gian Franco invece ragiona così:
Sovrappongo la base del triangolo al lato del rombo, però non ha la stessa lunghezza, la base è più corta e quindi un pezzetto del lato del rombo rimane non sovrapposto. Quel pezzo più l’altro lato, sono i 7 cm in più del perimetro del rombo rispetto a quello del triangolo. Se aggiungo i 3 cm che ho sovrapposto ho 10 cm. Quindi i lati obliqui insieme sono di 10 cm e il lato singolo di 5 cm. In tutto i due lati obliqui più la base di 3 cm fa perimetro 13 cm.
Il ragionamento di Gian Franco risulta più chiaro con l’immagine:
Aggiungo infine che Matteo, sempre della prima, ha risolto il quesito, ma andando per tentativi: ha attribuito diverse misure ai lati del triangolo isoscele fino a che: ho risolto solo quando il triangolo doveva avere perimetro 13 cm, il parallelogramma 16 e il rombo 20 cm. E va beh! 
Per la seconda risolvono: Gabriele G., Bachisio e Pietro S.
Gabriele fa un ragionamento simile a quello di Gian Franco, Pietro scrive (io aggiusto un po’ la forma):
per trovare la base del triangolo ho agito sul parallelogramma ruotando il lato obliquo fino a sovrapporlo alla diagonale. Ciò che resta sono i 3 cm in più del perimetro del parallelogramma rispetto al perimetro del triangolo. La base del triangolo è di 3 cm.
Invece per trovare la misura dei lati uguali: se da 7 sottraggo 3 e divido per 2, ottengo quanto misura in meno la base rispetto al lato, quindi il lato misura: 3+2= 5 cm, il perimetro quindi è 13 cm. [anche il ragionamento di Pietro si comprende meglio osservando la figura che illustra quello di Gian Franco]
Bachisio invece ragiona commentando le immagini [e sì, ma io sono costretta a costruirle, lui scarabocchia sul foglietto, oltre che intervenire sul suo italiano!]
i lati contrassegnati alla stessa maniera si ‘’annullano’’ a vicenda, del parallelogramma rimane un lato che è la base del triangolo: 3 cm.
Per il lato:
come sopra “annullo” i lati uguali nelle due figure quindi due lati del rombo superano di 7 cm la base del triangolo. Posso scrivere una formula:
l+l = b+7
b= 3 cm, quindi l+l=3+7=10 cm
il perimetro del triangolo è l+l+b = 13 cm
Possiamo passare al
quesito 2, sulle strette di mano.
Per la prima, risolvono: Miriam, Alessia, Giuseppe P., Elisa, Daniele, Arianna, Matteo, Gian Franco (ma, Gian Franco, la soluzione promessa via e-mail non l’hai poi consegnata?).
Tutti risolvono alla stessa maniera: contano da ciascun banco le strette di mano possibili evitando le ripetizioni.
Lo schema di Alessia sintetizza i ragionamenti seguiti. Il numero su ciascun banco indica le strette di mano che ciascuno studente scambia con i compagni dei posti adiacenti.
Gabriele G. e Bachisio della seconda impostano un ragionamento più rapido:
gli alunni con i banchi "agli angoli" (4) stringono la mano a tre compagni, quindi 4*3 =12 strette di mano
gli alunni con i banchi al "perimetro" (6), esclusi gli angoli, stringono la mano a cinque compagni ciascuno, quindi 6*5=30
gli alunni con i banchi al centro (2) stringono la mano a otto compagni ciascuno, quindi 2*8=16 strette di mano
Sommando 12+30+16 otteniamo 58, ma abbiamo contato due volte ogni stretta di mano. Quindi basta dividere per 2: 58/2=29
Bachisio raccoglie il tutto in un’espressione:
[(4*3)+(6*5)+(2*8)]/2=29
29 sono le strette di mano totali
Manuel e Davide A. risolvono con i conteggi dei compagni della prima.
Finito? Mi pare di sì. Bene e bravo come sempre a chi ha risolto ma anche a chi ci ha provato pur non giungendo alle giuste conclusioni. Ce lo siamo già detto ma lo ripetiamo: possiamo pure non riuscire a risolvere un problema, non è così importante, ma, se ci siamo concentrati su di esso ragionandoci su, possiamo dire comunque di ‘’essere cresciuti un po’”! Senza ansie, senza paure!
Alla prox, dal prof Davide!
Post
Tutti i commenti
