Ed ecco,
dopo ben due settimane di tempo, le nostre soluzioni al “Sarà mica matematica 23” di prof Davide.
Il tempo è stato dunque abbondante tanto da permettere una partecipazione numerosa! Sarà così? Vediamo ...
Quesito 1
Per la classe prima hanno risposto correttamente ... solo Gianfranco! Ehmmm, numerosa, cominciamo bene 
Bè, è così, per i ragazzi di prima il quesito ha presentato difficoltà. Gianfranco ha trovato le tre soluzioni raccomandate dal prof. Davide:
18654, valore doppio di 9327
18546, valore doppio di 9273
14658, doppio di 7329
La classe seconda se l’è cavata meglio. Danno più soluzioni: Bachisio, il più prolifico, Marco, Pierluigi, Gian Mario, Gabriele, Manuel, Pietro P. e Vincenzo. Riporto, in unico elenco, le soluzioni trovate:
18.654 - 9327
18.546 - 9273
14.658 - 7329
14.586 - 7293
13.458 - 6729
13.854 - 6927
15.846 - 7923
13.584 - 6792
14.658 - 7329
14.586 - 7293
15.864 - 7932
14.538 – 7269
Bachisio scrive anche come ha ragionato per risolvere il quesito:
Ho pensato che il numero doppio dovesse essere di 5 cifre, che terminasse con cifra pari essendo un doppio, che iniziasse con la cifra 1 perché sommando due cifre l’unico riporto può essere 1. Quindi avevo 4 cifre pari da utilizzare per la prima posizione (unità) del numero doppio. Escludo la cifra 2, perché doppio di 1, che serve per le decine di migliaia del numero doppio. Poi ho fatto un po’ di combinazioni seguendo una logica. Per esempio ho capito che il 7 poteva abbinarsi al 4, il 5 al 2, per avere:
5 4
2 7
ecc..
Quesito 2
Qui anche la classe prima è stata brava. Hanno dato la soluzione completa: Miriam, Gianfranco, Alessia, Elisa, Arianna, Cristina, Giuseppe P., Cristiana.
Giuseppe F. e Erika individuano diversi quadrilateri ma non tutti. (Ragazzi, se dimentico qualcuno, segnalate)
Per la classe seconda hanno risposto: Bachisio, Bruno, Pietro S., Davide A (1), Marco, Pierluigi, Gian Mario, Gabriele, Manuel, Pietro P.
Vincenzo individua una parte dei quadrilateri.
... Che sono complessivamente 12: lavorando sull’esagono regolare si individuano sei rombi e sei trapezi isosceli.
Alcuni alunni di entrambe le classi hanno riportato la soluzione in una animazione GeoGebra. Ho dovuto scegliere quella da pubblicare! Devo dire che i ragazzi della prima sono stati appena più precisi nella costruzione. Se poi si tiene conto anche della loro minore esperienza con GeoGebra ...
Quindi la scelta cade sui lavori della prima. E, fra questi? Ambarabà ciccì coccò ... è uscito il lavoro di Miriam! 
Clic su immagine
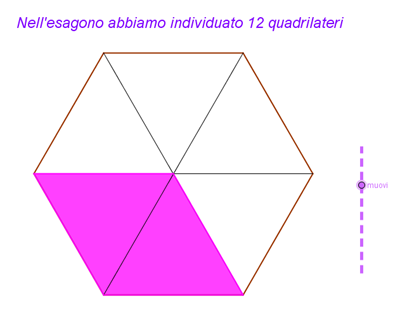
Mi piace aggiungere che, in seconda, questo gioco ci ha dato modo di studiare meglio l’esagono regolare. Abbiamo dimostrato che i triangoli in cui l’esagono è suddiviso, sono equilateri. E quindi come 6 dei quadrilateri individuati siano dei rombi e 6, dei trapezi isosceli. Abbiamo visto l’esagono inscritto in una circonferenza... Insomma, Grazie, prof Davide!
Concludendo, bravi tutti!
State in guardia: entro domattina, qui il nuovo Sarà mica... !



























