I punti notevoli del triangolo
sono proprio piaciuti!
Tanto che Gabriele (II) ha indagato per conto suo e in Rete ha scoperto il punto di Fermat.
Gabri scrive:
Fermat volle chiedere a Torricelli se era in grado di trovare un punto che rende minima (o minimizza) la somma delle distanze dai vertici di un triangolo qualsiasi.
Torricelli rispose: “bè, ma minimizza la distanza da ogni lato, no?”
- ah, rispose così?
Fatto sta che:
Il punto di Fermat (F) individua la distanza minima: se sommo la distanza da ogni vertice al punto di Fermat, rispetto a tutti gli altri punti all'interno del triangolo ottengo la somma minima.
Si ottiene costruendo in ogni lato del triangolo un triangolo equilatero, poi traccio tre segmenti che uniscano ogni vertice del triangolo di partenza con il vertice del triangolo costruito sul lato opposto, per esempio A con A_1.
Una volta fatto questo i tre segmenti si incontrano in un punto: il punto di Fermat, che è anche il punto di intersezione delle tre circonferenze circoscritte ai tre triangoli equilateri.
Ecco l’immagine della costruzione:
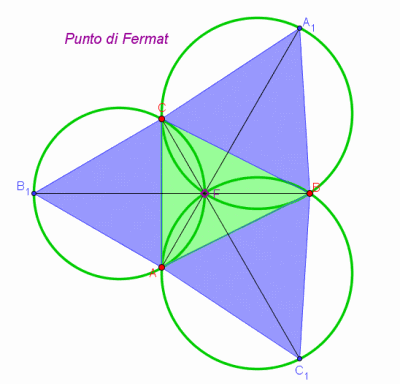
Bene, Gabri! In classe abbiamo per ora verificato, misurando con geogebra, che il punto di Fermat minimizza la somma delle distanze dai tre vertici del triangolo.
Utilizzeremo il tuo lavoro per approfondire: dovremo dimostrare perché AA1= BB1= CC1. Voi, chi può, cominciate ad osservare, attentamente, i triangoli ACA1 e B1CB ....
Ancora, sulla costruzione verificheremo le proprietà dei quadrilateri inscritti in una circonferenza. Osservate: AB1CF, AFBC1 e ...
Ma, ma... dicevamo nel titolo del post: c’è anche un punto di Gabri!
Sì, Gabriele ha voluto sperimentare. E ci dice:
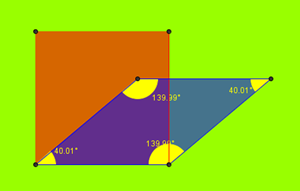
Ho tracciato le perpendicolari ai lati AC e BC del triangolo ABC, passanti per i punti (vertici) A e C (lato AC) e B e C (lato BC) del triangolo.
Ho segnato i punti C, E, F, G, le intersezioni delle perpendicolari.
Con dei segmenti ho unito i punti C, E, F, G e ho ottenuto un parallelogramma.
Nel caso del triangolo isoscele il parallelogramma è un rombo.
Quando il triangolo è rettangolo con l' angolo retto sul vertice C si ottiene un rettangolo.
Quando invece il triangolo è rettangolo isoscele con l'angolo retto sul vertice C, si ottiene un quadrato.
Il punto di incontro delle due diagonali del parallelogramma l’ho chiamato punto Gabri.
Osservando il caso dei triangoli rettangoli, ma con l’angolo retto su qualsiasi vertice, ho notato che il punto Gabri coincide con il circocentro del triangolo, perché cade sul punto medio dell’ipotenusa. Quindi ho tracciato la circonferenza circoscritta.
Perciò mi è venuto in mente che il mio punto potrebbe essere un altro modo per costruire il circocentro di un triangolo.
Clic sull’immagine per aprire l’applet GeoGebra con le costruzioni di Gabriele.





















![P12-10-10_11.53[1] P12-10-10_11.53[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjrWrYg2YU5myGEG2-fm7KOOASHKFJGFpTBoRd49jBRk1GB-8PpiHLIY1qXnABvz3f_Hl2fAgB5YTKGJBJ6r54MY1HcKwXxC2E4rhHjR8yY2xTBqRVsDK8Q4_i1jlZNMrsvoFHdqlHNoNo/?imgmax=800)
![P12-10-10_11.54[1] P12-10-10_11.54[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEgw9c2AC8AnDK6PEhO6AY1IK4fF_aZ4G12NalqYMaEM2YuFxVVF8xuTwKRQrTzVxfAbS3k5NrpecoHgy0wbVGWmMEe4X_22jvAoetv6IHBI38HDr8ZI6AgPSwWgap66m1d4xXWGbqfTWCY/?imgmax=800)
![P12-10-10_11.54[2] P12-10-10_11.54[2]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEiIshZtSfbLuBwoT1gUbI3oL1MXNT0q6I4EFOxDirpJDhLKretic_Kj_ZTYXt-pFH-MW9Hl5vU1sDs50yp72tWVYXHK9V1ynuo20P3Yi3-m-phgR5F-_d2zUx5_EF4sxCr_iT2evE-uPik/?imgmax=800)