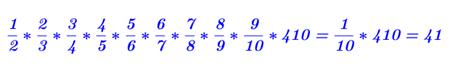Questo il primo post-soluzioni dell’anno
dei giochi matematici Lombardia-Sardegna! Sì, sì, solo due scuole e solo due corsi ma sempre di Lombardia-Sardegna si tratta.
Il Sarà mica matematica 41 del prof. Davide è piaciuto e non è stata male la partecipazione. Ha impegnato i giovini quanto basta e soprattutto questo è positivo.
Ed ecco le soluzioni e i solutori.
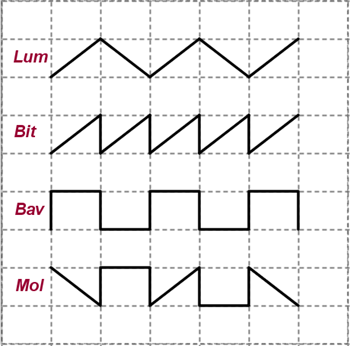
Quesito 1, la sequenza numerica
41 5 46 10 56 …
la logica (o le logiche) che porta(no) ai successivi numeri.
Hanno risolto per la classe prima: Margherita (la prima a spedire la sua soluzione), Stefano P., Gabriella, Fabiano (alias Fabio), Sofia, Giorgia, Antonio, Andrea, Ludovica, Stefano B.
La soluzione più gettonata è stata quella del di 5 in 5 i numeri in giallo (nel post originale del prof.) e i numeri in arancio si ottengono sommando i due numeri che li precedono.
Fabio e Gabriella trovano due soluzioni, la miglior risposta è quella di Stefano P. che trova tre logiche:
Ho pensato che si potrebbe risolvere in 3 modi:
• Se i numeri in rosso aumentano di 5 in 5, quelli blu si ottengono sommando i due numeri che li precedono:
41 5 46 10 56 15 71 20 91 25….
Secondo questo ragionamento il numero che sta alla decima posizione è 25 [altri prolungano la successione...]
• Se i numeri in rosso raddoppiano di volta in volta e quelli blu si ottengono sommando i due numeri precedenti avremo:
41 5 46 10 56 20 76 40 116 80….
In questo caso il decimo numero è 80
• I numeri rossi si ottengono sommando le cifre del numero blu che li precede, mentre i numeri blu proseguono sommando di volta in volta quelli rossi che si ottengono:
41 5 46 10 56 11 67 13 80 8….
Alla decima posizione avrò il numero 8
Per la classe seconda risolvono: Marta C., Maria (le prime due soluzioni-Stefano), Yuri, Davide, Margherita, Elena, Elisa, Paola, Andrea (tre soluzioni), Roberta, Aurora, Nicol, Valentina (tre soluzioni), Martina (due soluzioni).
Riporto le tre soluzioni di Valentina (miglior risposta. A pari merito con Andrea ma con un qualcosa in più. Anche nella spiegazione, in cui Andrea tende sempre a fare economia):
prima soluzione:
si può notare che la differenza tra 41 e 46 è equivalente al numero che sta in mezzo, ossia 10; ho notato che 5 e 10 sono multipli di 5, e quindi ho trasformato la sequenza inserendo i segni:
41+5= 46
46+10= 56
56+15= 71
71+20= 91
91+25= 116 (11° posizione)
seconda soluzione:
riprendendo le osservazioni precedenti, notiamo che 10 è il doppio di 5, quindi per questa soluzione ho preferito prima eseguire con le lettere:
a + x= b 41+5= 46
b + 2x= c 46+10= 56
c + (2x)•2 = d 56+20= 76
d + (2x)•4 = e 76+40= 116
e + (2x)•8 = f 116+80= 196 (11° pos.)
[… ha preferito. Bene, siamo solo in seconda, ci si avvia alla generalizzazione ...]
terza soluzione:
ho notato che la differenza tra 41 e 56 è la somma tra 5 e 10. Quindi ho ragionato: sommando il secondo addendo “giallo” con il primo e, al numero ottenuto aggiungendo il 2° addendo “arancio” ...:
41+5= 46
46+10= 56
56+15= 71
71+25= 96
96+40= 136 (11° posizione)
Andrea riporta le tre soluzioni-Valentina
Martina riporta la I e la III delle soluzioni-Stefano
Quesito 2, … con le frazioni
Quanto è
1/2 di 2 /3 di 3/4 di 4/5 di 5/6 di 6/7 di 7/8 di 8/9 di 9/10 di 410?
Eh eh, prof. Davide, Stefano P. della prima ha notato che il 41 tornava più volte nella puntata N° 41 
Ma andiamo per ordine.
Dalla classe prima ricevevo le e-mail: “Invio le risposte al I e al III. Le frazioni non le ricordo!”
Ma arriva poi la risposta di Fabio mediante foto dal quaderno:

E bravo Fabio! Ma, ovviamente, la prof. alla classe: carissimi, se Fabio ha ricordato, voi altri …. ?
Ha funzionato, è tornata la memoria!
Quindi per la prima risolvono: Fabio, Margherita, Sofia, Antonio, Stefano P., Gabriella, Ludovica e Stefano B.
Margherita, Ludovica e Stefano B. come Fabio,
Copio-incollo la mail di Sofia:
1/3 2/3 3/4 4/5 5/6 6/7 7/8 8/9 9/10
semplifico le frazioni e ottengo 1/10; 1/10 di 410 fa 41
Le devo dire la verità, in questo quesito mi ha aiutato un po' mamma ma l'ho capito subito.
Antonio così:
Ho fatto 1/2 per 2/3, il risultato per 3/4, poi l'ho semplificato e moltiplicato ancora per 4/5 e ho continuato così fino ad ottenere 1/10 di 410 e sono arrivato ad ottenere 41 come risultato finale.
In seguito aggiunge:
Il modo per risolverlo l'avevo capito, solo che mamma mi ha detto di semplificarle perché cosi mi veniva più facile fare le moltiplicazioni e ho visto che c'era la sequenza da 1/2 ad 1/10.
Stefano P. scrive:
Ho iniziato facendo 410 : 10 = 41 x 9 = 369 [lascio passare, non è corretto scrivere quegli “uguale” a catena!] e ho continuato a calcolarmi il risultato delle frazioni finché ho capito che la differenza tra ogni risultato che ottenevo era di 41. Quindi ho ottenuto 41 nove volte, perciò se faccio 41 x 9 ottengo 369 che devo sottrarre al 410. Ho ottenuto di nuovo il numero 41!!!
Il numero 41 è proprio in rosso nella sua e mail. E in classe mi dice: io mi sono accorto che il 41 nei giochi non appare solo nel primo quesito…
Gabriella scrive:
prima ho eliminato i numeri doppi lasciando 1 e 10 gli unici non doppi
1/2 2/3 3/4 4/5 5/6 6/7 7/8 8/9 9/10
quindi prendendo 1/10 di 410 basta fare 410:10 = 41
Ho chiesto qualche chiarimento ma si limita a sottolineare con il rosso … mah!
Per la classe seconda, i solutori: Paola, Andrea, Roberta, Sara, Aurora, Marta C., Margherita, Elisa, Maria, Elena, Antonio, Yuri, Valentina, Martina.
Quasi tutti impostano la soluzione mediante espressione. Che realizzano poi su Geogebra utilizzando La Tex (eh, sono in seconda, hanno imparato). Così:
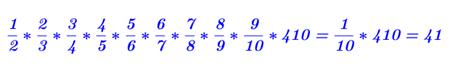
O così: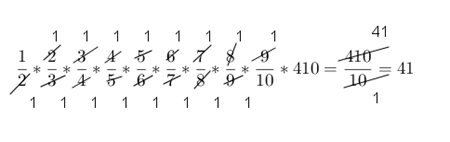
Paola scrive anche una risposta diversa, seppure un po’ contorta, io modifico appena quando proprio non è comprensibile!
La risposta è 41. Faccio dapprima: 410/10 = 41, 41×9 = 369.
Quindi al 410 gli è stato tolto 41 (ho moltiplicato per 9 e non per 10, quindi è come che [SE!] io avessi fatto 410-41= 369).
Poi anziché fare 369:9×8= 328, faccio 369 - 41= 328. Quindi non calcolo nove volte la frazione dei numeri ottenuti ma faccio:
410-(41×9)=410-369=41.
Andrea:
bisogna "solo" dividere per 10 il 410, perché guardando bene le frazioni si nota che le cifre dal 2 al 9 sono prima usate come denominatore di una frazione e poi come numeratore , quindi si semplificano a vicenda, e la frazione finale sarà 1/10. 1/10 di 410 = 41.
Roberta:
Innanzitutto ho guardato attentamente le frazioni, mi è venuto subito in mente che la prof. ssa ci aveva detto che applicando la frazione operatore è come moltiplicare per la frazione, quindi il "di" si trasforma in "per". Allora mi sono scritta l’espressione: 1/2*2/3*3/4*4/5*5/6*6/7*7/8*8/9*9/10 * 410; Ho notato che ogni frazione era semplificabile a croce, es:1/2*2/3 = 1/3. Seguendo questo ragionamento, nell'ultima frazione avrò: numeratore 1 e denominatore quello dell'ultima frazione, 10. Alla fine mi sono ritrovata con 1/10*410= 41.
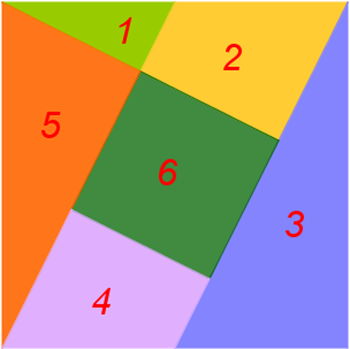
Quesito 3, i ponti di Konigsberg, semplificati e non …
Solutori per la prima: Stefano P., Gabriella, Fabio, Sofia, Giorgia, Andrea, Ludovica, Stefano B.
Per la seconda: Paola, Andrea, Roberta, Sara, Aurora, Marta C., Margherita, Elisa, Maria, Elena, Antonio, Yuri, Valentina, Martina e Nicol.
Risolvono tutti il problema dei 5 ponti, con diverse soluzioni. Mi è arrivato di tutto, disegnini su carta, foto e file con foto su cui sono tracciati i percorsi. Privilegio questi ultimi nel pubblicare, per ovvi motivi.

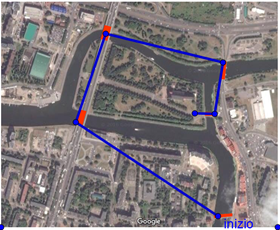
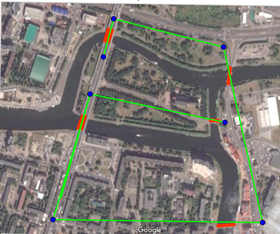
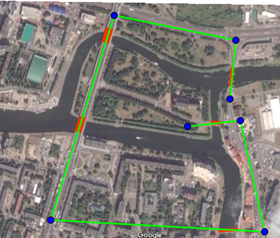
etc, etc…
Per ciò che riguarda i 7 ponti qualcuno dice: non si può passare in tutti i ponti senza attraversarne uno 2 volte.
Poi qualcun altro, in prima: se i ponti fossero 6 oppure 8 il percorso si potrebbe fare.
Infatti, bravi primini!
Fabio e Sofia inviano le due soluzioni alternative
Fabio invia il disegno:
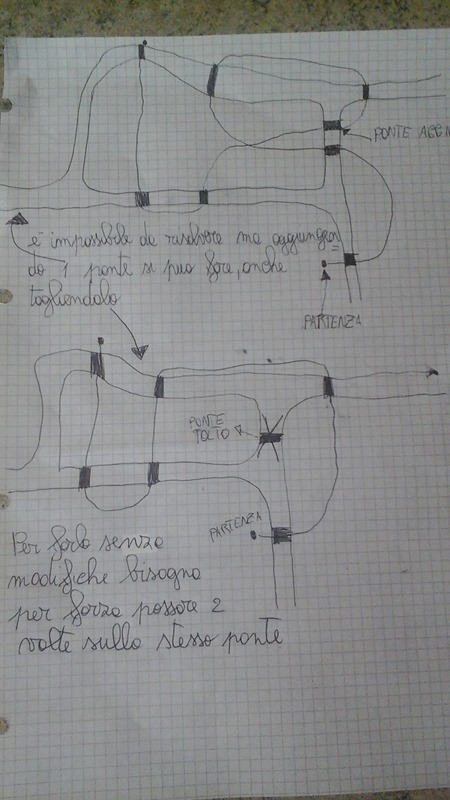
Sofia, che dice:
per quanto riguarda i 7 ponti di Konigsberg li ho osservati bene e basandomi su qualche frase del prof. Davide ho fatto qualche ricerca e ho trovato che molte persone provavano a fare il percorso passando in tutti i ponti ma senza passare più volte su un ponte, e nessuno ci riusciva, quindi ho pensato che non si può fare.
Ma con 6 ponti:

e con 8 ponti:

sì!

Infine, anche Roberta, della seconda, fa una ricerca sui 7 ponti di Konigsberg. Trova che del problema si è occupato il grande matematico Eulero che formulò delle leggi un pochino difficili per la soluzione del problema. Ma dichiarò che con 7 ponti era impossibile!
Beh, Robi, il materiale che hai trovato non era semplice.
Ragazzi, se siete curiosi e volete sapere un po’ di più sul problema dei ponti impossibili, provate a vedere due post sul blog:
Gioco topologico e Scopri la formula di Eulero!
Bene, mi pare di aver concluso. Come sempre, se ho scordato qualcosa o qualcuno, segnalate!
E come sempre, il mio Bravi! a tutti i solutori. A chi si è impegnato, a chi ci ha provato, a chi non molla mai!
E Grazie! al prof. Davide.
Oh, scordavo: fra qualche giorno qui per i nuovi giochi!