Trasformazioni geometriche a confronto

L’idea è di Davide D.

Che mi invia un file dove vuol mostrare come la rotazione di 180°, la simmetria centrale e l’omotetia inversa di rapporto uguale a –1, corrispondano alla medesima trasformazione geometrica nel piano, rispetto a uno stesso centro.

Davide osserva però: l’omotetia è un movimento più elastico perché dilata o rimpicciolisce l’oggetto.

Quanto alla costruzione ... ho deciso di intervenire massicciamente su quella di Davide. Che proprio bella bella non era! Ma, guai a Davide se non impara : studia (studiate!) la costruzione da Proprietà! Ok, qualcosa chiariremo insieme ... Questo lavoro, consideriamolo di Davide e della prof!

E dunque, guardate l’applet. Clic su figura o, come al solito Download

Per la I A _Movimenti nel piano

Ragazzi,

eccovi i link promessi.

QUI ... sorpresina.

Poi QUI. Cliccate sempre sulle immagini ... dopo aver letto si intende! Fate anche gli “esercizietti”!

Se trovate difficoltà nell’aprire le applet, ditemi quali!

E poi QUI.

Una volta aperte le applet premete, se non sempre è indicato, sul pulsante Play in basso a sinistra.

Per cominciare basta questo. Voi, bè, vedete un po’ voi!:-)

Un esercizio ...d'obbligo!

Ragazzi belli...
bisogna assolutamente andare ad eseguire l'esercizio proposto da maestra Renata. Ehi, i ragazzi della sua V, primaria, lavorano sulle isometrie! E vedrete.... :-)

Isometrie | Splash ragazzi via kwout

grazie maestra Renata!

La simmetria centrale

III,
cominciamo dunque ad approfondire il discorso sulla simmetria.
Meglio, sulle simmetrie...
Come accennato QUI, conosciamo un po' la simmetria per aver incontrato in diversi contesti, figure (o tabelle) che ... si guardano allo specchio, qualche esperimento concreto in classe è capitato anche in questi giorni. Il ribaltamento come movimento rigido, appartiene alle isometrie ed è una particolare simmetria.
In questo post non vi faccio lavorare ancora su quella particolare simmetria.
Intendo riprendere la domanda posta sull'ultima attività nel foglio di lavoro geogebra(tornateci!)
Ma ... cominciamo così:
osservate questa bella Rosa di Grandi a 4 petali

Ho fissato il punto centrale C, disegnato poi un punto A sulla curva e, mediante lo strumento

Simmetrico rispetto a un punto, ho individuato appunto, il simmetrico, punto A', del punto A rispetto al centro C.
[vi guido con l'immagine:

Strumento, clic sul punto A (oggetto da trasformare), clic su C, centro di simmetria]
Nella rosa abbiamo dunque individuato una simmetria.
Propriamente, si tratta della simmetria centrale:
il punto A' è il punto corrispondente nella simmetria centrale di centro C, al punto A
Ora, fate clic sulla rosa e andate a muovere con il mouse il punto A sul petalo.
Osservate, agite e riflettete:
- il punto A', suo simmetrico rispetto al centro, descrive il petalo simmetrico della curva;
- confrontate le distanze AC e A'C. Potete misurare: strumento Distanza o lunghezza, questo lo conoscete! Cosa osservate?
- i punti corrispondenti A e A' sono allineati. Uniteli usando lo strumento Segmento tra due punti.
- Il punto C dunque, rispetto al segmento AA', cosa rappresenta? Dovrete usare un altro strumento per verificare ...
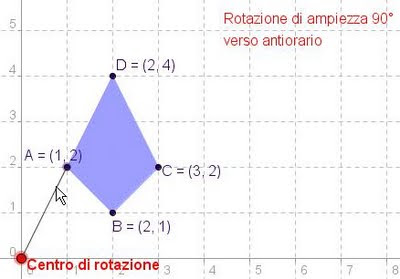
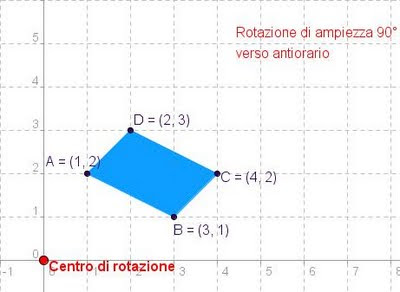
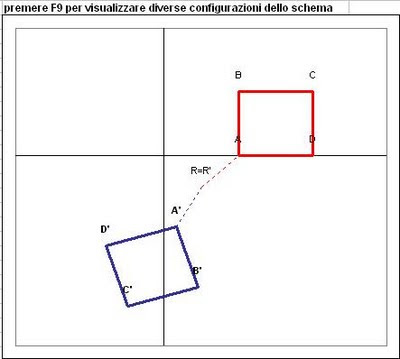
In quest'ultima domanda dovreste riconoscere quella cui accennavo sopra... (ultimo lavoro sulla rotazione)
Rivediamo l'immagine:

La rotazione di ampiezza α=180° ha caratteristiche diverse dalle altre rotazioni:
- i punti corrispondenti A e A', B e B' .... sono allineati con il centro E;
- EA = EA'
- E è quindi il punto medio dei segmenti di estremi A e A' , B e B', ...
Una domanda: nella rotazione di 180°, quale parte ha il verso della rotazione? Come deve o può essere? Ripetete l'attività! :-)
Per le caratteristiche descritte i punti A e A', ecc..., corrispondenti nella rotazione di 180°, si dicono simmetrici rispetto al punto E (centro di simmetria).
Due punti qualsiasi P e P' si dicono simmetrici rispetto a un punto O (il centro di simmetria) se O è il punto medio del segmento PP'.
Dunque concludiamo che:
ogni rotazione nel piano di ampiezza α=180° attorno a un centro O, è una simmetria centrale, o simmetria di centro O.
Possiamo anche dire che la simmetria centrale coincide con la rotazione di 180° rispetto al centro di simmetria!
Dobbiamo ora imparare a costruire il simmetrico di un punto rispetto a un altro, centro di simmetria. Vedremo poi la simmetria centrale dei poligoni e individueremo le coordinate sul piano cartesiano.
Alla prox!

La rotazione sul piano cartesiano in Geogebra

III A,
dopo quello della traslazione, eccovi lo studio della rotazione sul piano cartesiano.
Per individuare le coordinate dei vertici di un poligono ruotato di una certa ampiezza rispetto a un altro, dato il centro di rotazione e il verso, sul vostro quaderno dovreste utilizzare riga e squadra e in alcuni casi goniometro (in quali casi?). Con Geogebra invece... osservate come si fa nel seguente filmato. Clic sull'immagine

Ora provate voi sull'applet. (Potete sempre tenere aperta anche la finestra del filmato, potete bloccare, tornare indietro, riattivare...)
Clic per aprire la finestra del foglio di lavoro:

In un secondo foglio potete seguire mediante slider la rotazione di un quadrilatero, in senso orario oppure antiorario, confrontare le coordinate dei vertici con i risultati del precedente lavoro, osservarne la variazione a seconda dell'ampiezza di rotazione.
Particolare attenzione va prestata alla rotazione di 180°. Vedi foglio di lavoro.
In proposito ... c'è da sviluppare lo studio delle trasformazioni geometriche! Clic:

Buon lavoro!
(oops, devo ancora vedere i lavori di Anna Laura! fra un po', bella! :-))

Esercitazioni con Geogebra sulla traslazione

III A,
come promesso pubblico le esercitazioni guidate da fare on line sul foglio di lavoro dinamico di Geogebra.
1) Come fareste sul vostro quaderno, applicare la traslazione di vettore $\vec{ u }$ assegnato, ad un poligono ABCD e visualizzare le coordinate dei vertici A', B', C', D' . Clic sull'immagine per aprire il video che vi mostra come fare con Geogebra

Ora esercitatevi sul foglio di lavoro. Clic:

2) Per la seconda esercitazione non è necessario guidarvi. Sono sufficienti le indicazioni riportate sul foglio di lavoro. Siete avvantaggiati rispetto al lavoro sul quaderno!
Si tratta di stabilire (ma è solo una verifica, le coordinate le vedete indicate) la relazione tra le coordinate x e y, dei vertici di un poligono e quelle, x', y', del poligono ad esso corrispondente nella traslazione di vettore dato, tenuto conto delle dimensioni del rettangolo di cui il vettore è la diagonale. Dovete riportare sul vostro quaderno le relazioni trovate dopo ogni modifica del vettore.
(vi ricordo: A(x;y) ----> A'(x ± b_rett; y ± h_rett) così per gli altri vertici; il simbolo ± indica più (+) oppure meno (-), dipende dalla direzione e dal verso del vettore. vero?)
Sul foglio trovate le indicazioni per modificare direzione, verso e intensità (o modulo) del vettore. Clic sulla figura e buon lavoro!

La rotazione in Excel

Dopo la traslazione, la rotazione in Excel.
Ma questa ... farina d'altrui sacco!:)
Dal mago dei grafici (e non solo) Fernando Cinquegrani, ho trovato il lavoro pronto per noi.
Clic sulla figura per scaricare il file rotazioni2d.xls

Al link si arriva da QUI, dove già si possono visualizzare diverse applicazioni realizzate da Fernando. In fondo alla pagina cliccate su
contributi ai newsgroup (alcuni)
contributi ai newsgroup (molti altri)
per trovare, e scaricare, numerosi esempi in risposta ai più svariati quesiti posti da utilizzatori di excel, nei newsgroup appunto.
Dunque, lavoro già pronto, ma ho voluto anch'io, giusto sulla falsariga, riprodurre la rotazione di figure sul piano.
Un triangolo:

un altro quadrilatero:

Il file da scaricare rotazione.xls
grazie Fer!

La traslazione in Excel

Ragazzi, ripasso o studio qui e ora
la traslazione sul foglio elettronico Excel.
questa l'immagine, clic per ingrandire

Il foglio contiene le indicazioni per modificare il triangolo di partenza, le coordinate degli estremi del vettore, quindi la sua lunghezza, e volendo si può modificare anche il verso della traslazione.
Le verifiche confrontano:
la lunghezza del vettore con la distanza tra i punti, AA', BB', CC', corrispondenti nella traslazione;
e controllano:
la direzione della traslazione mediante il calcolo della "pendenza", quindi del coefficiente angolare, di due rette, quella contenente il vettore e quella contenente il segmento AA': rette con uguale coefficiente angolare sono tra loro parallele.
Il file da scaricare Traslazione.xls

Rotazione: individua il centro e...

Sempre dopo QUESTO e QUESTO, stavolta in particolare per quanto concerne la rotazione,
ancora un'esercitazione guidata.
Si tratta di:
individuare il centro, l'ampiezza e il verso della rotazione che fa corrispondere una figura F' a una figura F.
Naturalmente con GeoGebra, seguite prima come si fa, nel filmatino.
clic sulla figura

Ora, a voi sull'applet. Clic

Dopo aver eseguito gli esercizi ....
VERO o FALSO?
1. Il centro di rotazione è sempre esterno a una figura F
2. Il centro di rotazione può coincidere con un vertice di un poligono F
3. In una rotazione R₀ il centro di rotazione è equidistante da due punti corrispondenti di F e F'
E ancora, per accertare meglio conoscenze e linguaggi ...
4. Una rotazione è una isometria diretta
5. Se F' e F si corrispondono in una rotazione, allora F' e F sono direttamente congruenti.

Disegna il vettore

Ragazzi, non prima di aver "studiato" QUI e QUI, in particolare la parte relativa alla traslazione,
ecco una piccola (facile) esercitazione. Guidata!
Con l'aiuto della nostra amica maestra Renata, che ringrazio tanto, posso pubblicare un piccolo video - tutoriale che vi mostra come operare per eseguire l'esercizio che vado a proporvi.
Disegnare, con GeoGebra, il vettore che in una traslazione di alcune figure piane fa corrispondere la figura F' alla figura F
Seguite come si fa, nel filmato. Clic sull'immagine.

Tutto chiaro?
Ora, fate voi sull'applet GeoGebra. Clic

Buon divertimento! :-)
[Aggiornamento]: ancor di più potete divertirvi con le Traslazioni con i vettori di Maestra Renata. E non trascurate di guardare il video:
Inserimento di un vettore tra due punti e traslazione con i vettori, che già avevo segnalato in un precedente post.
Renata, felice dell'interazione, scambio, continuità in verticale! :-)

Proprietà della traslazione e della rotazione

Continuiamo la nostra attività sui movimenti nel piano.
Abbiamo visto delle proprietà comuni alla traslazione e alla rotazione: avvengono nello stesso piano nel quale giace l'oggetto e sono movimenti rigidi che conservano invariate forma e dimensioni dell'oggetto (le figure ottenute con i due movimenti sono congruenti), traslazione e rotazione sono trasformazioni geometriche definite isometrie.
Ora studiamo le proprietà che distintamente caratterizzano le due trasformazioni.
Come al solito utilizziamo GeoGebra, cominciamo con la traslazione.
Clic sulla figura per aprire l'applet e ... scoprire!:

E la rotazione:

Ragazzi, vi segnalo Inserimento di un vettore tra due punti e traslazione con i vettori, un video della maestra Renata che vi sarà di grande aiuto per comprendere meglio la traslazione. Anzi direi che sarebbe da vedere prima!
Attenzione, sulla pagina troverete più di un video, tutti interessanti, dovreste vederli... : quello che ci interessa nel caso specifico è il terzo, insomma basta leggere :-)

Movimenti nel piano

Ragazzi, ricordate i pesciolini nell'acquario ...cartesiano?
Ah, se non li ricordate ... perché non li avete visti :-(
dovete fare il clic e andare a vedere.
E comunque,
guardiamoci questi due

Lo sapete che il pesciolino azzurro non è altro che quello rosso che nuotando ... ha cambiato colore?[perché i nostri pesciolini sono cangianti! :-) ]
Nel post, quello su cui siete andati a vedere, avevo accennato alla geometria delle trasformazioni. Dovremo occuparcene, come vi ho detto, in maniera da fare ordine...
Già conosciamo (un po'), trasformazioni che non deformano in alcun modo le figure, cioè che fanno ottenere delle figure congruenti a quella iniziale, figure che si sovrappongono punto per punto, combaciano... Lo abbiamo visto tante volte ruotando degli oggetti, es la squadretta, per cambiare la posizione di angoli ..., oppure osservando delle figure o delle tabelle o parti di tabelle che si guardano allo specchio ..., e abbiamo detto che si tratta di movimenti rigidi.
Il nostro pesciolino nuota in un mare che, in matematica, chiamiamo piano cartesiano.
Cominciamo dunque a conosce meglio i movimenti nel piano (in quello cartesiano in particolare, in un secondo momento, )
E, a proposito di movimento, non potendo stare ferma, ho preparato delle animazioni!:-)
Cliccate: osservate che il triangolo T si muove, scorrendo sul righello. Il movimento è chiamato traslazione.

La traslazione avviene nel piano stesso nel quale giace il triangolo T. E' una proprietà specifica della traslazione.
Ora un altro movimento. Il triangolo è fissato alla lancetta delle ore di un orologio. La lancetta ruota ...

La rotazione, come la traslazione, avviene nel piano stesso nel quale giace il triangolo T.
Infine, un altro movimento rigido: nell'animazione vedrete la figura F che si trasforma in quella F', mediante un ribaltamento.

Il movimento di ribaltamento avviene fuori dal piano in cui giace la figura F (apri il palmo di una mano: per sovrapporlo al palmo dell'altra devi eseguire un ribaltamento, movimento fuori dal piano che contiene la prima mano)

Ora, mettiamo giusto un po' d'ordine, curando un po' la terminologia specifica:

1) Movimento rigido: traslazione, rotazione e ribaltamento;
le figure ottenute mediante questi movimenti si sovrappongono perfettamente, punto per punto, alla figura di partenza; esse sono congruenti. Le due figure congruenti mantengono quindi invariate ogni lunghezza, l'ampiezza degli angoli, l'estensione nel piano (area). Si dicono perciò isometriche (dal greco, di uguale misura - iso, ricordate, isoscele...- ).
La traslazione, la rotazione e il ribaltamento sono delle trasformazioni geometriche definite isometrie.
2) La traslazione e la rotazione avvengono nel piano nel quale giace la figura iniziale: sono detti movimenti diretti; le figure ottenute con questi due movimenti si dicono direttamente congruenti (o direttamente isometriche)
3) Il ribaltamento è un movimento inverso: richiede di uscire dal piano in cui giace la figura iniziale.; le figure ottenute per ribaltamento sono dette inversamente congruenti (o inversamente isometriche).
E... vi sarete accorti che il ribaltamento lo abbiamo già conosciuto con il nome di simmetria (figure che combaciano, si guardano allo specchio...) Ma è una particolare simmetria... su queste dobbiamo indagare più a fondo!
Per il momento fate qualche esercizietto:
a) Osserva le tre figure

__ __

In quale figura osservi:
- Una traslazione? .........................................
- Una rotazione? ..........................................
- Un ribaltamento? ......................................
Quale dei tre movimenti non è avvenuto nel piano nel quale giace la bandierina alla sinistra? ...............
Infine va', due schede da ingrandire e stampare, per sapere ...

e per saper fare

Testo di riferimento per l'argomento e le attività: Matematicamente - Ed scolastiche B. Mondadori da cui sono tratte schede e immagini.

Pesciolini nell'acquario ... cartesiano!

Ragazzi,
vedete questi bei pesciolini colorati?
Fate clic. Vedrete quello rosso solo soletto, agite sul pulsante Play, l'acquario cartesiano si popolerà!

E' solo un giochino, tanto per introdurre la geometria delle trasformazioni: similitudine, traslazione, rotazione, simmetrie...
Abbiamo più di una volta solo accennato a queste trasformazioni. Ora c'è da fare ordine, distinzioni, approfondire insomma, e imparare a operare! E, vedete, può davvero essere divertente.
Vabbé... per quest'anno scolastico non si fa in tempo. Potete però cominciare ad indagare... quando avrete voglia, durante le vacanze!:-)