Costruzione delle classi di equivalenza

Ragazzi,

abbiamo visto le classi di equivalenza. Quegli insiemi, infiniti, di frazioni equivalenti, ciascuno dei quali è un numero razionale: una classe di equivalenza <--->un numero razionale.

Cioè: più rappresentazioni, come frazione, dello stesso numero razionale.

L’insieme dei razionali, dunque, l’inseme Q è costituito da tutte le classi di equivalenza, dall’insieme delle classi di equivalenza.

Eh, fermiamoci solo un attimo: Un insieme, Q, infinito, i cui elementi sono degli insiemi, infiniti ... ancora una volta incontriamo ...l’infinito!

E ora, vediamo:

le classi di equivalenza sono insiemi infiniti. Come abbiamo fatto con i numeri naturali (N), infiniti, possiamo rappresentarle mediante un ente geometrico, infinito naturalmente: la retta.

Precisamente:

ogni classe di equivalenza può essere rappresentata come una retta, passante per l'origine degli assi cartesiani, che passa per ogni coppia ordinata che rappresenta quel numero razionale.

Ricordate le coppie ordinate? Ricordate il prodotto cartesiano? (fate clic sui link!)

In questo caso le coppie ordinate in questione le possiamo rappresentare così:

$(a,b) ---->  \frac{ a }{b} \,=\,\frac{k*a }{k*b }$

il numero k è un naturale qualsiasi (proprietà invariantiva, vero?).

Il sistema di riferimento cartesiano ci aiuta nella rappresentazione grafica delle classi di equivalenza.

Vediamola. Clic sull’immagine per aprire l’applet geogebra.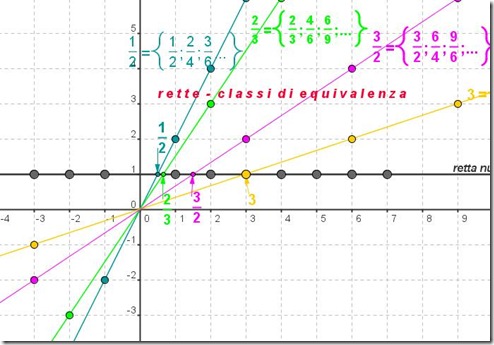a)  Tutte le rette (tranne quella numerica, dei naturali e ...) passano per l’origine degli assi cartesiani;

b) ogni punto di ciascuna retta ha per coordinate una coppia ordinata di valori che corrisponde a:

 $(a,b) ---->  \frac{ a }{b} \,=\,\frac{k*a }{k*b }$ (a/b = k*a/k*b)

Come fare per ottenere la retta che rappresenta una classe di equivalenza?

Qualche esempio: volete rappresentare il numero razionale 3/5?

Sulla barra di inserimento digitate: x =3/5 y e, invio.

Per individuare – evidenziare dei punti che formano la retta:

digitate sulla barra di inserimento: (3, 5) e, invio; o anche (6, 10), invio. (Naturalmente anche il punto (1.5, 2.5) – ho diviso per 2 - farà pare della retta!) Ecc...

Volete rappresentare il numero razionale 4?

Sulla barra di inserimento digitate: x = 4 y

Per evidenziare dei punti sulla retta:

sulla barra di inserimento: (4, 1), O anche: (8,2), ecc...

Potete provare subito anche sull’applet.