Pubblico
la soluzione del quesito data da Beatrice, su GeoGebra.
Clic per aprire l’applet

Davide D. risolve, ma non spiega. Mi è piaciuta la sua idea di ricomporre le quattro figure, a formare il quadrato, con la traslazione. La vediamo in figura.

Aggiorno il post con la soluzione del primo quesito del problema, discussa nella classe III. Relazionano Maria Chiara e Letizia
Dopo le soluzioni dei ragazzi di seconda, ecco che arriva anche la nostra.
Come vuole la prof abbiamo lavorato non più secondo l’intuizione, ma dando una spiegazione ad ogni conclusione: *dimostrare* !
1) Trovare le misure incognite dei lati dei triangoli e del pentagono su riportato.
Iniziamo con le misure più facili da trovare.
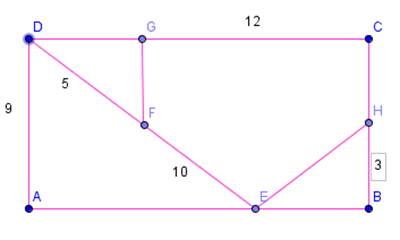
CH = CB-HB = DA-HB = 9-3 = 6
In quanto CB è uguale a DA poiché sono lati paralleli, quindi congruenti, dello stesso rettangolo
DE = DF+FE = 5+10 = 15
Avendo così la misura di DA e DE che costituiscono cateto e ipotenusa di un triangolo rettangolo possiamo trovare AE :
$AE = \sqrt{DE^2-DA^2}=\sqrt{15^2-9^2}=\sqrt{225-81}=\sqrt{144}=12$
Ancora osserviamo:
DG = EB in quanto AE = GC e AB = CD
Ora però viene la parte più complicata, dove bisogna utilizzare concetti studiati precedentemente:
come facciamo a trovare DG?
Sappiamo solo che esso è uguale a EB ma essendo anche questo incognita non può esserci d’aiuto così la prof ci invita a focalizzare la nostra attenzione sui triangoli DAE, retto in A, e DGF, retto in G.
Dopo un minutino di silenzio ecco che Erica interviene aprendo la strada a tutti con un’osservazione molto acuta e utile per arrivare ad una soluzione. Riporto qui sotto:
< il triangolo DGF è ⅓ di DEA>; infatti la misura del lato DF (5) e la misura del lato DE(15) sono in rapporto 1:3.
Bene ma, l’affermazione di Erica, dice la prof, non è sufficiente a stabilire che "il triangolo DGF è ⅓ di DEA" . Continuiamo quindi a "studiare" i due triangoli.
Essi possiedono un angolo retto in quanto sono dei triangoli rettangoli, ma abbiamo notato che hanno anche un secondo angolo uguale, ecco il disegno qui sotto:

Gli angoli segnati in verde sono uguali perché alterni interni: prolungando i lati AB e DC da entrambi i vertici avremmo le rette parallele, la trasversale è data dal prolungamento del segmento DE da entrambi gli estremi.
Ora possiamo dire che se hanno 2 angoli uguali anche il terzo sarà uguale in quanto la somma degli angoli interni di tutti i triangoli è di 180°.
Adesso abbiamo tutte le condizioni per poter affermare che i due triangoli (DAE e DGF) sono simili secondo il primo criterio di similitudine: due triangoli sono simili quando gli angoli corrispondenti sono congruenti, ma in questo caso potremmo anche dire “due triangoli rettangoli sono simili quando hanno uno dei due angoli acuti congruente”.
Quindi i loro lati sono in proporzione. Perciò possiamo scrivere:
DG : AE = DF : DE
DG : 12 = 5 : 15
DG = 12*5/15 = 4
Una volta trovata la misura di DG (e anche di EB) possiamo trovare con il teorema di Pitagora anche i lati HE e GF:
$HE=\sqrt{EB^2+HB^2}=\sqrt{4^2+3^2}=\sqrt{16+9}=\sqrt{25}=5$
$GF=\sqrt{DF^2-DG^2}=\sqrt{5^2-4^2}=\sqrt{25-16}=\sqrt{9}=3$


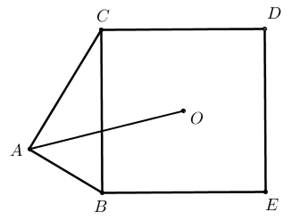
 Esercizio n. 1 – In parti uguali?
Esercizio n. 1 – In parti uguali?