Ragazzi,
Vi ricordo l’impegno di un’altra scoperta: la “regola” che permette di disegnare delle figure senza mai sollevare la matita dal foglio e…
Siete a buon punto: avete già verificato che a volte le figure si possono costruire, altre volte no, rispettando le condizioni!
In “Gioco topologico” vi ho detto anche che avremmo conosciuto una formula, la formula di Eulero, che in qualche modo potrebbe aiutarvi nel gioco topologico!
Intanto: Eulero? Questo nome non vi è nuovo vero? Sì, è proprio l’Eulero dei diagrammi di Eulero-Venn, che utilizziamo per rappresentare graficamente gli Insiemi!
Leonhard Euler, italianizzato in Eulero, è il matematico svizzero vissuto nel ‘700, il cui nome è legato a “una lista impressionante di formule, teoremi, metodi, criteri, relazioni, equazioni...” !
Non studiò solo matematica, ma anche astronomia, biologia e tecnologia…
Per conoscerlo meglio andate a leggere
I "signori" Eulero e Venn
e anche
Ancora un omaggio a Eulero
Nel campo della matematica Eulero aveva un sacco di idee! Tra le altre cose, disegnava dei punti che congiungeva con delle linee. E facendolo si mise a pensare a un possibile legame tra il numero di spigoli e il numero di vertici nelle diverse figure.
Eulero chiamava spigoli le linee e vertici i punti in cui si incrociano le linee. Indicava anche come regioni le parti di piano racchiuse dalle figure e quelle fuori da esse.
E trovò il legame tra vertici, spigoli e regioni! Contando il numero di vertici, il numero di spigoli e il numero delle regioni (dentro e fuori dalle figure, ricordate!) verificò che il risultato dell’operazione:
n° Vertici - n° Spigoli + n° Regioni
che, essendo un matematico, indicò con i simboli:
V – S + R
è sempre uguale a ….
andrete a scoprirlo!
Oggi, quasi 300 anni più tardi, la formula di Eulero, è una formula importante, usata tra l’altro in topologia. Per l’appunto!
La quantità: V-S+R viene detta anche “Caratteristica di Eulero” e la formula fu formulata anche per i poliedri, i solidi geometrici, e perfino per altre superfici come la sfera, ecc…
E ora, a scoprire la “caratteristica di Eulero” !
Clic sull’immagine per aprire l’applet GeoGebra. Stavolta utilizzerete anche il foglio di calcolo. E’ disponibile anche in Geogebra, lo sapevate?

Home page * GeoGebra * Excel * Matematica nella Storia. I Grandi Matematici * Matematica ricreativa * Libri * Le Curve Celebri * Immagini per la Matematica * Tutoriali * Le Formule più belle * Matematica e ... *
Altri modi per visualizzare il blog
INFORMATIVA SULLA PRIVACY E SUI COOKIE
*MATERIALE DIDATTICO *Risorse didattiche e SCUOLA *BLOG DIDATTICI e colleghicheleggo *Risorse EXCEL - OFFICE *Info CREARE e ARRICCHIRE IL PROPRIO BLOG *Altro Blogroll *Condivisioni *Visualizzazione formule matematiche
domenica 31 gennaio 2010
Scopri la formula di Eulero!
Etichette: Caratteristica di Eulero, Eulero, geogebra, matematica ricreativa, topologia
sabato 30 gennaio 2010
Videotutorial utilizzo Equation Editor
Ragazzi,
in questo video vi mostro come si può utilizzare Equation Editor, uno strumento per scrivere formule ed espressioni matematiche, che troviamo in Word e, inserito come "Oggetto", possiamo utilizzare anche in Excel.
Vediamo nell'esempio come eseguire un'espressione aritmetica con le potenze.
Attenzione: vi ricordo che nell'esecuzione delle espressioni con le potenze, sono valide le stesse regole che abbiamo visto con i naturali ma c’è una regola in più: l'elevamento a potenza ha la precedenza su tutte le altre operazioni.
Scegliete la visualizzazione a schermo intero
Nota: dopo l'immissione di ogni esponente occorre premere il tasto freccia a destra. Così anche per passare fuori dalle parentesi.
Etichette: Equation Editor, Tutoriali, video
venerdì 29 gennaio 2010
Videotutorial Testo dinamico con Geogebra
Testato velocemente il suggerimento di oggi di prof Daniele:
ScreenToaster, registra e pubblica le tue lezioni
Ho creato un piccolo video che illustra come creare un testo dinamico con GeoGebra .
Precisamente: visualizzare in un testo, dinamico, il rapporto tra le misure di due segmenti.
Non è il caso più semplice, ma è quanto mi è venuto in mente ... per fare in fretta! :-)
Cliccate sulla visualizzazione a schermo intero.
Etichette: testo dinamico con GeoGebra, Tutoriali, video
Gioco topologico
Ragazzi (di prima),
Avvio qui un’attività ricreativa che realizzeremo poi tutti insieme. Intanto chi legge può cominciare …
Siete capaci di disegnare questa figura senza mai sollevare la matita dalla carta e senza mai ripassare su una delle linee?
Riuscite a disegnarla senza alzare la matita dal foglio e senza ripassare su alcuna delle linee?
Quando avrete trovato la soluzione, provate voi a inventare delle figure.
Da disegnare sempre senza mai sollevare la matita e senza ripassare su nessuna delle linee.
Ecco qualche altra proposta: alcune di queste figure non si possono disegnare senza mai alzare la matita. Quali sono?
Questo è un gioco topologico: ha a che fare con spigoli e angoli. Cioè con il modo in cui si congiungono dei punti con delle linee, come si fa con una formula, la formula di Eulero, che conosceremo meglio in un altro post.
Avete dunque un piccolo suggerimento: evidenziate i punti che congiungono le linee (tutte le linee, rette e curve) o in cui le linee si incontrano e provate a individuare qualche differenza, o caratteristica … Potete schematizzare i risultati in una tabella:
| figura | qui il disegno o denominazione (a, b,…) | disegno o … |
| caratteristica | ? | ? |
| può essere disegnata senza …. (SI’ o NO) |
Attività da “Ce li hai i numeri?” Editoriale scienza
Topologia: significa letteralmente studio dei luoghi (dal greco τοπος (topos), luogo, e λογος (logos), studio).
È anch’essa una branca della matematica. La topologia generale (o topologia degli insiemi di punti) definisce e studia alcune proprietà utili degli spazi e delle mappe, come la loro connessione, la continuità …
Intanto potete anche cominciare a leggere e a giocare con Case, pozzi, strade, ponti... !
Etichette: Eulero, Giochi, matematica ricreativa, topologia
giovedì 28 gennaio 2010
Il comportamento delle potenze nelle 4 operazioni
Così ha intitolato Letizia
il suo lavoro in Excel sulle 4 operazioni con le potenze. Dimostra quando si possono applicare le proprietà – scorciatoie e quando no.
Ecco qualche immagine d’esempio

Si può scaricare il file proprietà_potenze.xls
Leti, hai utilizzato il SE() logico, brava!
Ma! :-)
Tu prova ad es. in cella C30 a cancellare la base scelta; e controlla che succede nelle celle F30 e J30 (allarga le colonne).
Cosa manca al tuo SE() ??
Abbiamo detto che:
noi possiamo dire: “SE domani farà bel tempo, (allora) andrò a fare una passeggiata in pineta”
Excel vuole invece sapere anche cosa farò Se il tempo non sarà bello!
… altrimenti mi risponde un po’ sgarbato! ;-)
Etichette: alunni, Esercitazioni, Excel, Potenze, Proprietà delle potenze
martedì 26 gennaio 2010
Soluzione Enigma poligoni simili
La soluzione all’enigma è stata data da Dario nei commenti.
Due poligoni simili non possono sovrapporsi in maniera tale che l’ingrandimento copra perfettamente il poligono più piccolo solo se si tratta di poligoni concavi (QUI e QUI).
E’ necessario, come ben afferma Dario, che su due vertici consecutivi l'angolo interno del poligono sia maggiore di 180 gradi, vale a dire tre rette passanti alternativamente su altrettanti lati suddividono il poligono in due parti ciascuna delle quali si trova su due distinti semipiani.
La condizione non è tuttavia sufficiente. Influisce anche l’ampiezza degli angoli consecutivi a quelli della concavità, come dimostrano le figure seguenti.
In questa il poligono A’ copre perfettamente il poligono simile A. - Cliccando sull’immagine si può aprire l’applet GeoGebra, verificare e provare a modificare le costruzioni.
In quest’altro caso invece non è possibile coprire il poligono B con quello simile B’.
Etichette: enigmi della matematica, matematica ricreativa, Similitudine
domenica 24 gennaio 2010
L’enigma dei poligoni simili
Per i ragazzi e per … i più grandi!
come c’è da aspettarsi, in qualsiasi maniera li sovrapponiamo, il più grande ricopre sempre perfettamente il più piccolo.
Ma, ma … :
ho due poligoni simili; quando cerco di coprire il più piccolo con il più grande, non ci riesco. Non c’è verso !
Siete in grado di spiegare perché ?
(non vale dire che ho sbagliato la costruzione!:)
Etichette: enigmi della matematica, matematica ricreativa, Similitudine
sabato 23 gennaio 2010
Qualche esercizio sulla similitudine
Ragazzi,
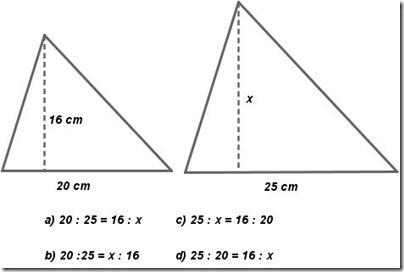
provate ad eseguire i seguenti semplici esercizi sulla similitudine. Sono tratti da diversi “Test prova Invalsi”.
1. Osserva i due triangoli simili e scegli la proporzione che ti permette di calcolare il valore x
2. I due triangoli isosceli ABC e A’B’C’ sono simili.
Qual è la misura dell’angolo al vertice A’B’C’ ?
3. I due pentagoni regolari P e P’ hanno i lati, ridotti in scala ovviamente, che misurano rispettivamente 5 cm e 20 cm.

A – 1/3 B – 3 C – 1/5 D - 5
b) Qual è il rapporto fra l’area del secondo, A’, e quella del primo, A ?
A - 1/3 B – 3 C – 1/9 D – 9
4. Osserva le figure: quale dei due trapezi Tr’ e Tr’’ è simile al trapezio Tr ?
Etichette: esame terza media, Esercitazioni, Similitudine
venerdì 22 gennaio 2010
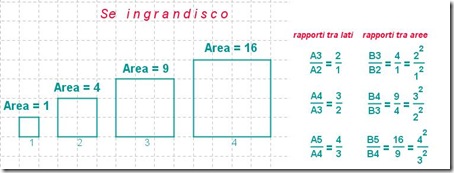
Similitudine e rapporti tra aree
Ragazzi,
abbiamo già visto la relazione tra lato e area di un quadrato, assieme a quella tra raggio e area del cerchio.
Di recente le abbiamo considerate nello studio delle funzioni matematiche…
Riconsideriamole ora alla luce di quanto sappiamo sulla similitudine.
In due figure simili è costante il rapporto tra lati corrispondenti, cioè essi sono in proporzione. Inoltre sono congruenti gli angoli corrispondenti.
E il rapporto tra le aree di due figure simili?
Sull’applet di GeoGebra lavorerete sui quadrati, ma la regola che scoprirete se è valida per i quadrati lo è anche per i rettangoli simili;
e se vale per i rettangoli vale anche per i triangoli simili, perché un triangolo è sempre la metà di un rettangolo;
e se vale per i triangoli vale anche per i poligoni simili, perché …. Perché?
Etichette: geogebra, rapporto tra aree figure simili, Similitudine
giovedì 21 gennaio 2010
Potenze di 10
Ragazzi della prima!
Vi facilito il lavoro di ricerca sul blog secondo indicazioni date, con i link su potenze e curiosità, sulla barra a destra In evidenza per la I A. Elenco numerato!
Nel ricordarvi il link che troverete su potenzedi10.xls, eccovi un altro bel video sulle potenze di 10, segnalato tempo fa da Gravità Zero, blog di divulgazione scientifica.
Un viaggio immaginario dall'infinitamente grande all'infinitamente piccolo scalando una potenza di 10 ogni 2 secondi. Dai confini dell'Universo all'interno degli atomi.
UN VIAGGIO FANTASTICO NELL'UNIVERSO CONOSCIUTO
un altro video da non perdere: “Mi raccomando, guardatelo al buio e, per godervi a pieno lo spettacolo, portatelo a tutto schermo nella versione in alta definizione!”
Etichette: Potenze, potenze di 10, video
martedì 19 gennaio 2010
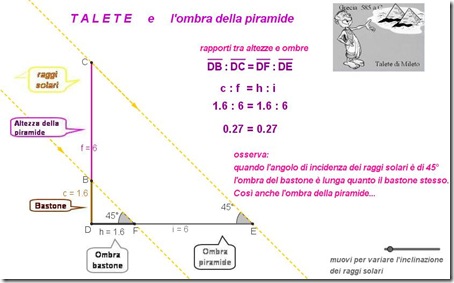
Talete e l’ombra della piramide
Talete di Mileto,
lo abbiamo incontrato QUI … in Egitto, a sbalordire sacerdoti, re e storici, con la misura dell’altezza della piramide!
A questo punto dovremmo essere in grado di comprendere meglio per quale motivo Talete poteva affermare che ad una determinata ora del giorno, l’altezza della piramide era uguale alla lunghezza dell’ombra o che, se l’ombra del bastone era doppia della lunghezza del bastone, altrettanto accadeva all’ombra della piramide rispetto all'altezza della piramide.
Osserviamo un’immagine:« ... Piantata un'asta al limite dell'ombra proiettata dalla piramide, poiché i raggi del sole, investendo l'asta e la piramide formavano due triangoli, [ha] dimostrato che l'altezza dell'asta e quella della piramide stanno nella stessa proporzione in cui stanno le loro ombre.» (Plutarco)
Naturalmente alla lunghezza dell’ombra della piramide va aggiunta la distanza fra il centro della base della piramide e il lato su cui si proietta l’ombra.
E, ricordiamo:
la direzione dell’ombra gira durante il giorno e la sua lunghezza cambia e il tutto è ancora diverso nei diversi giorni dell’anno (immagine dalla Rete)
(QUI, da maestra Renata, in fondo alla pagina - Le stagioni - un’interessante applet: si può osservare l’inclinazione dei raggi solari a diverse latitudini e nei diversi mesi dell’anno).
Per osservare la relazione matematica esistente tra altezze e ombre degli oggetti, aiutiamoci come al solito con la costruzione dinamica: riproduciamo con Geogebra l’esperimento di Talete.
Al variare dell’ombra degli oggetti, il rapporto tra le ombre resta costante e tale rapporto è uguale a quello delle loro altezze (i raggi del sole si considerano paralleli).
Tutto ciò non è altro che un'altra importante applicazione del Teorema di Talete, attribuito proprio al filosofo scienziato di Mileto, secondo il quale:
un fascio di rette parallele individua su due rette trasversali, coppie di segmenti direttamente proporzionali.
Nel caso della misura dell’altezza della piramide, il fascio di rette parallele è costituito dai raggi solari, le due trasversali sono la retta a cui appartengono le altezze del bastone e della piramide e la retta che contiene i segmenti - ombre.
Studiate sull’applet. Clic sulla figura:
Etichette: geogebra, Similitudine, Talete, Teorema Talete
domenica 17 gennaio 2010
Similitudine e omotetia con GeoGebra
Ragazzi,
ripartiamo dall’attività precedente per approfondire l’indagine sulle figure simili.
Stavolta occorre parlare di …numeri! Se vogliamo essere precisi nell’ingrandimento e nella riduzione di figure, bisogna imparare a costruire una figura simile a una data secondo un certo rapporto.
Il rapporto di similitudine tra un poligono A e un poligono B può essere:
- maggiore di 1: allora A è un ingrandimento di B
- uguale a 1: allora A è congruente a B
- minore di 1: allora A è una riduzione di B
Comprenderete meglio naturalmente, aiutati da GeoGebra.
Sull’applet trovate diverse attività:
- costruzioni sulle quali agire per osservare proprietà varianti e invarianti;
- “adesso prova tu”: utilizzando gli strumenti a disposizione costruirete voi figure simili, guidati dagli esempi;
- un quesito per verificare la comprensione: utilizzando lo strumento Testo darete la vostra spiegazione;
- infine, si precisa il concetto di *omotetia*.
Due figure simili possono non essere omotetiche. Il termine omotetia deriva dal greco e significa “che ha la stessa posizione”. Per il modo in cui due figure simili sono costruite, non solo hanno la stessa forma ma hanno anche la stessa posizione: le coppie di lati corrispondenti sono parallele fra loro.
- Sarete guidati passo a passo anche alla costruzione di figure simili omotetiche.
Riflettete, utilizzate informazioni precedenti, cercate di porvi domande e di rispondere a quelle sollecitate!
Ma … andiamo a lavorare sull’applet!
L’immagine illustra il quesito… Clic su di essa. Avviate l’attività da m=0! :-)
Etichette: attività interattiva, geogebra, omotetia, Similitudine
giovedì 14 gennaio 2010
Ingrandimenti e riduzioni
Ragazzi,
Cominciamo a ragionare sulle similitudini. Lo studio ci aiuterà a precisare i due concetti fondamentali (non solo per la matematica) di forma e dimensioni di un oggetto o di una figura, chiarendo che queste due caratteristiche sono indipendenti una dall’altra.
Le similitudini sono trasformazioni che mantengono la forma di una figura pur cambiando le sue dimensioni. Perciò sono trasformazioni non … ? Dunque dobbiamo ben distinguerle dalla grande famiglia delle … ? !
Osservate intanto qualche figura.
Per costruire i modellini-giocattolo di un’automobile viene fatta una riduzione
Una fotografia si può ingrandire
Le carte geografiche si costruiscono in scale diverse
La similitudine la troviamo anche nell’arte: sotto, un’opera dell’artista olandese M. C. Escher (già incontrato qui).
Ma come si ingrandisce o rimpicciolisce una figura?
Aiutiamoci con GeoGebra naturalmente! Clic sulla prima immagine e … buon lavoro sull’applet. Per ora niente numeri! Se occorre, visualizzate “Griglia”.
Un ingrandimento - riduzione
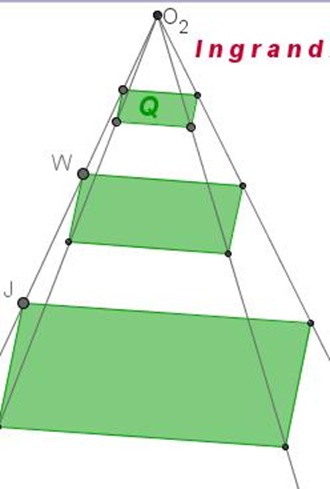
Etichette: geogebra, ingrandimenti e riduzioni, Similitudine
Le girandole!
E sì, i monellini di prima si divertono proprio con GeoGebra.
E’ la volta di Letizia, che gioca con cerchi, archi e slider! (Bèh, ci siamo divertiti un po’ tutti in classe a ruotare … di un certo angolo … proprio come questi bei bimbi!:-) [ragazzi, dovete andare a vedere i video. Cliiic!]
Etichette: alunni, animazioni, geogebra, Giochi
martedì 12 gennaio 2010
Un problema: corda e circonferenza su piano cartesiano
Ecco l’altro esercizio eseguito con GeoGebra da Sara.
clic sull’immagine per aprire l’applet
Etichette: alunni, geogebra, problema sulle corde, Sistema di riferimento cartesiano
lunedì 11 gennaio 2010
Talete di Mileto – altra lettura propedeutica …
Ragazzi,
Ecco un altro bel salto nel passato. E che passato! Parliamo dell’antica Grecia, quell’affascinante culla della civiltà e della cultura, che nella storia della matematica occupa un posto di primo piano.
Un’altra lettura propedeutica, per parlare di similitudine.
Osservate un attimo la linea del tempo e … immergetevi!
Le figure che hanno la stessa forma ci sono così familiari che nemmeno ci sembra possibile che ad esse siano collegati dei problemi matematici.
« Si vede - diciamo – che quei due oggetti hanno la stessa forma » ; " si vede " che quando proietto una diapositiva su uno schermo parallelo la figura è sempre la stessa ma molto ingrandita; " si vede " che mentre gonfio un palloncino di gomma sul quale è disegnato un pupazzo, questa figura diventa via via più grande ma è pur sempre lo stesso pupazzo.
Il nostro occhio è così preso dalla figura che non viene spontaneo di associare al fatto visivo, qualitativo, un fatto quantitativo, cioè una legge matematica. Eppure, le origini della similitudine come teoria matematica vanno cercate in tempi molto molto lontani:
« Io soprattutto vi ammiro, Talete di Mileto, perché, ponendo il vostro bastone all'estremità dell'ombra di una piramide, formaste coi raggi del sole due triangoli, e dimostraste che l'altezza della piramide sta alla lunghezza del bastone come l'ombra della piramide sta all'ombra del bastone ». Così scrive lo storico greco Plutarco vissuto nel I secolo dopo Cristo.
Ma, chi era Talete? e, che cosa significa esattamente quella frase di Plutarco?
Talete era nato a Mileto, città greca dell'Asia Minore, intorno al 625 a. C.; la città era in quel tempo un centro agricolo importante e una delle colonie della Grecia che più si distinguevano per i commerci e le industrie.
Oggi Mileto è una piccola cittadina della Turchia; del suo antico splendore rimane solo traccia nelle rovine di imponenti costruzioni messe in luce in seguito agli scavi iniziati alla fine del secolo scorso. E dagli scavi è risultato anche che la città era un tempo costruita in modo geometrico, tipo scacchiera: i caseggiati erano tutti estremamente regolari e le strade si tagliavano ad angolo retto, proprio come nelle moderne città americane.
Vivendo in questo centro in piena fioritura economica era naturale che il giovane Talete si dedicasse ai commerci; ed è appunto per questo che si recò in Egitto. Si racconta – ma è una leggenda che ha certamente un fondo di verità storica – che passeggiando nella zona delle piramidi
in compagnia di due sacerdoti, questi ragionassero su come sarebbe stato possibile calcolare l’altezza di quelle colossali costruzioni (notate che ancora non si conosceva il Teorema di Pitagora, che permette il calcolo assai semplice dell’altezza di una piramide).
Immediatamente il giovane Talete intervenne nei discorso dicendo che la cosa gli sembrava facilissima: bastava infatti conficcare nella terra un bastone ed aspettare il momento in cui l’ombra del bastone fosse uguale alla lunghezza del bastone. In quello stesso momento - disse - l'ombra della piramide sarà uguale all'altezza della piramide; e così, con una semplice misura eseguita sul terreno, sapremo l'altezza della piramide.
Ma poi soggiunse che non occorreva aspettare l'istante in cui l’ombra del bastone fosse uguale al bastone stesso; è infatti evidente che se l’ombra del bastone risulterà doppia del bastone, altrettanto accadrà all’ombra della piramide rispetto all'altezza della piramide; se l'ombra del bastone sarà tripla del bastone, anche l'ombra della piramide sarà tripla dell'altezza della piramide; se …
È evidente, sì, ma occorre pensarci ...
Questo episodio di leggenda e di storia che si è svolto sulle rive del Nilo segna il punto di partenza della teoria delle figure simili.
« Io soprattutto vi ammiro, Talete di Mileto, ... ». Dopo sette secoli così viene ricordato il primo scienziato della Grecia; un uomo che per le sue scoperte matematiche e astronomiche, per le sue indagini sui fenomeni naturali e sulla materia primitiva di cui sono costituite le cose, fu annoverato fra quelle personalità un po’ leggendarie che sono i sette saggi della Grecia.
Da La Matematica/la Geometria – E. Castelnuovo
Per sorridere un po’ riporto un aneddoto, già pubblicato QUI, su Talete di Mileto:
"Proprio all'inizio del pensiero occidentale [la storia della filosofia occidentale] esplode una sonora, cristallina risata di scherno nei confronti della scienza:
quella della servetta tracia [abitante della regione Tracia] che vide Talete [osservatore della natura, studioso delle stelle...], camminare a testa alta guardando le stelle e cadere in una buca" !
Etichette: matematica nella storia, Similitudine, Talete
sabato 9 gennaio 2010
Una ciambella …quasi toro !
Gabriele
qualche tempo fa si è divertito con GeoGebra ad animare dei cerchi!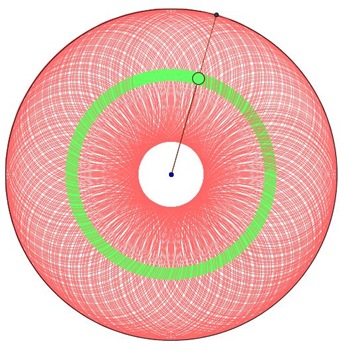
Clic sull’immagine.
Etichette: alunni, animazioni, geogebra, Giochi
venerdì 8 gennaio 2010
Ex 112 pag 36 !
Un compito per casa.
Sara, monella q.b., sì una monella di terza media, quando crede fa delle belle cose.
Ha eseguito con GeoGebra uno degli esercizi per le vacanze natalizie (anche qualche altro, ma da ritoccare!)
Si chiedeva la misura dell’area della parte colorata.
L’immagine dal lavoro, clic per visualizzare l’applet. Con dimostrazione!
Etichette: Esercitazioni, Esercizio geogebra, geogebra
giovedì 7 gennaio 2010
Esercitazione: le coppie additive e moltiplicative in Excel
Letizia,
ha lavorato sulle coppie additive nel piano cartesiano.
E anche su quelle moltiplicative…
Ecco le immagini del suo lavoro in Excel.
Letizia: come vedi ho aggiunto al tuo grafico una bella linea rossa, che è una vera linea curva. Sul tuo grafico hai una linea spezzata poiché hai quattro coppie di valori, quindi solo quattro punti.
La line rossa aggiunta prende il nome di linea di tendenza. Viene utilizzata proprio per visualizzare la tendenza dei dati di un grafico.
Il tuo grafico non è una linea curva ma tende a una linea curva! Ciò significa che:
aumentando il numero di coppie moltiplicative aumenta il numero di punti che, uniti, formano una linea sempre più curva….!
Osserva l’immagine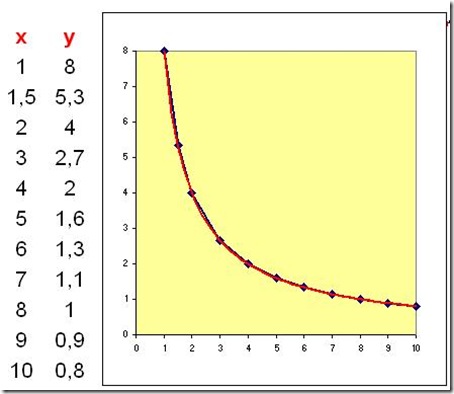
Ah, un’ultima cosa !
La curva ottenuta dalle coppie moltiplicative ha un preciso nome. Tutte le curve geometriche hanno dei nomi ben precisi! [ma qui sul blog avete visto o no? :-)]
Più precisamente la nostra curva è solo un ramo di una curva!
Il nome della curva … significa eccesso, esagerazione, amplificazione, ingrandimento …
Insomma provate a scoprire il nome!
Io sono certa che in classe ci arriviamo … :-)
martedì 5 gennaio 2010
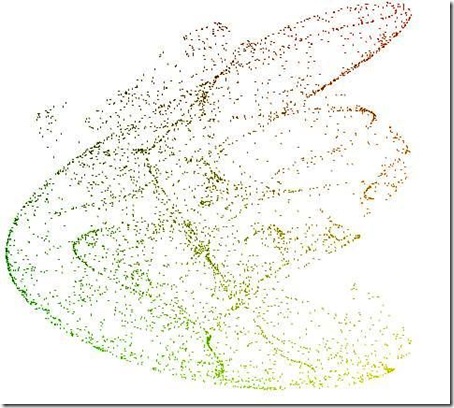
Attrattori (strani) in Excel [aggiornato]
Osservate, ragazzi e amici lettori
Ancora una volta il prof. Daniele suscita la mia curiosità!
Per la verità stavolta mi sfida lui a cimentarmi con geogebra nella realizzazione di questi fascinosi oggetti geometrici. Che sono gli attrattori, come spiega Daniele…
Ma questa volta ho rinunciato a geogebra (non so proprio se sia possibile con il software, non trovo alcun riferimento in Rete).
Epperò… c’è sempre Excel
… a saperlo gestire-dominare!
Qualcuno capace c’è! Si chiama Fernando Cinquegrani ed è un mago dei grafici! (non è la prima volta che mi aiuta qui!)
Tanto che… mi ha preparato QUESTO FILE
Sul foglio di lavoro è possibile variare i parametri a, b, c e d per ottenere diversi attrattori.
Per i valori dei parametri si veda questa pagina oppure questa.
Ecco qualche immagine del lavoro di Fer.
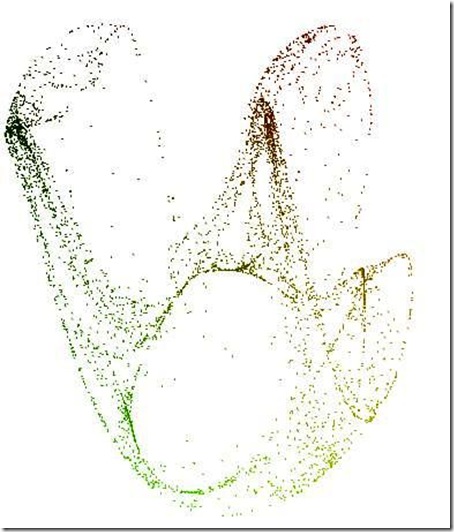
Ma c’è ancora un’altra cara amica, Barbara, geniale con Excel! (Barbara, Fer e altri amici sono stati i miei maestri di Excel. Non gli ho dato come alunna le soddisfazioni dovute! :-( Ma ho imparato moolto!)
Barbara ha realizzato Peter de Jong.xls
Ecco le immagini. Anche qui, si possono variare i parametri… 
a questi altri ho dato io il colore (e sono di un file precedente, che Barbara ha poi migliorato!). Il grigio tra l’altro, mi pare più bello.
Bèh, ditemi voi se non ho dei fantastici amici! :-)
g r a z i e, Daniele, Fer e Barbara!
[Aggiornamento]
C’è ancora un amico, Roberto, gentilissimo. Ha realizzato un’altra versione sugli attrattori.
Il suo file a questo link
Utilizzo: Attivate le macro, viene creata la barra per richiamare una userform. Si può scegliere il numero di punti desiderato e *Crea nuovo grafico*, successivamente *Aggiorna le serie*.
[Aggiornamento di Aggiornamento!]
Roberto si è appassionato gli attrattori :-)
e … “ho preparato una cartella di excel che consente di *giocare* nel vero senso della parola, con le curve di Peter de Jong ... poi ho trovato una variante e ne ho inventate altre due (la numero 3 e 4) giusto per rendere il gioco più vario”
Continuate a leggere sul suo blog. Potrete scaricare il file. Clic sull’immagine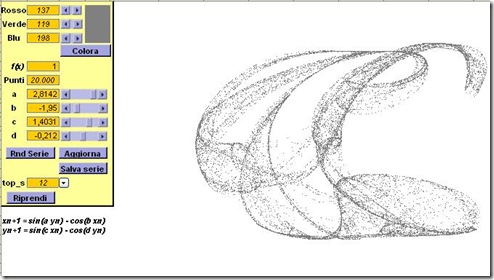
Ancora grazie Roberto. Davvero un bel lavoro!
Etichette: Attrattori strani, Excel, Peter de Jong