Spirale delle radici!

Appena ricevuta da Beatrice:

“Professore’ ho costruito la spirale delle radici su ggb seguendo le istruzioni del blog!!
Ciao!”

Clic per aprire l’applet. Con animazione o slider!

Sì sì, Bea hai seguito proprio bene le istruzioni. Brava!

Aggiungo la “chiocciola” di Davì

Non metto l’applet, ma ho controllato la costruzione: corretta! Bravo, Davì. Si impara, si consolida sempre qualcosa, a fare!

Esercitazione_Spirale_Teodoro

Marco D.  (I)

è stato molto bravo a costruire con Geogebra, rispettando le giuste perpendicolarità, il tipo di triangolo di partenza, ... , la

Spirale di Teodoro.

Conoscono, anche i ragazzi di prima, l’estrazione di radice come operazione inversa dell’elevamento a potenza, e a Marco è piaciuta tanto la spirale realizzata dai compagni della classe seconda.

Clic sull'immagine se volete scaricare il lavoro di Marco.

Marco? Bravo!

Spirali auree

Letizia (II),

da quella di Teodoro, è passata ad indagare su altre spirali e ha realizzato con GeoGebra ...

la spirale aurea

Corredata da piccolo commento:

In geometria la spirale aurea è una spirale logaritmica
(detta anche spirale equiangolare o di crescita), ovvero
un tipo di spirale che si ritrova spesso in natura (a me ha
ricordato le ammoniti fossili).
La spirale logaritmica è stata descritta la prima volta da
Descartes e successivamente indagata da Jakob Bernoulli,
che la definì spira mirabilis,la spirale meravigliosa, e ne
volle una incisa sulla sua lapide.

Letizia scrive poi:

... mentre curiosavo su internet ho scoperto che esiste anche una spirale aurea esterna e così ho pensato di riprodurre anche quella.

Ispirandomi alla successione di Fibonacci ho voluto realizzare una spirale aurea per ottenere una conchiglia particolare ormai estinta: l'ammonite.

Brava Letizia!

Per capire meglio il senso di spirale equiangolare, invito te e i tuoi compagni a leggere (eventualmente lavorare su ...):

La spirale equiangolare

Verso l’infinitamente grande!  (ritrovi le notizie sulla “Spira mirabilis”...)

Interessantissima anche la:

Spirale uniforme o di Archimede

La spirale aurea

Ah mi piace dirlo:
questi bambini della prima sono proprio bravi!
Marco D. ha visto il video del

Grande racconto della geometria

Mi dice come ha fatto e ...
“ Ho seguito la griglia, ho fatto una retta rispetto ad una linea orizzontale della griglia e poi ho misurato 21, poi ho tracciato una perpendicolare alla prima linea, e su di essa ho misurato 13; dal punto che delimitava i 13 quadretti ho fatto partire una perpendicolare, poi dalla fine del segmento 21, un'altra perpendicolare. Il punto d' intersezione e ho trovato il rettangolo, e così via.
L'idea mi è venuta quando lo scrittore ha parlato della successione di Fibonacci e il rettangolo aureo, cioè che togliendo un  quadrato si riusciva a ottenere un altro rettangolo in cui si può fare lo stesso procedimento.”
Ed ecco la spirale aurea di Marco. Io gli ho visualizzato punti e segmenti che lui lasciava nascosti (giustamente quasi, è così bella la spirale!) Clic

Bravo Marco!
PS: intanto lo stesso Marco e Beatrice, hanno realizzato il loro

Caleidoscopio

e devono salvare delle immagini....

Paperino e la matemagica!

Ragazzi,
Oggi è domenica e ... andiamo al cinema! :-)
Segnalati su PI GRECO QUADRO,
vi invito a godervi 3 fantastici video. Incontriamo

Paperino nel mondo della matemagica

Cominciate con questa 1* parte. I ragazzi di seconda ritroveranno magie di cui abbiamo già parlato, con quelli di prima avremo modo di scoprirle. Sul blog abbiamo notizie e attività, con voi cominciamo dal film!

Buon divertimento! In seguito, 2* e 3* parte.

La spirale ... da “riconoscere”

Ragazzi,
e ora la “sorpresa” fra le spirali equiangolari.
Osservate la figura

Ora non pensate all’angolo, alla suddivisione dell’angolo giro di cui abbiamo parlato finora.
Vi domando invece se la costruzione vi ricorda qualcosa...
Osservate in figura la serie di rettangoli. (La spirale passa però sui vertici di quadrati, voi concentratevi sui rettangoli) Mmh.. vi dice nulla? Pensateci un po’, su!
Ma se proprio avete il “vuoto”, sono certa che visualizzando l’animazione, riconoscerete ... !:-)

Verso l’infinitamente grande!

QUI, nella costruzione della spirale equiangolare, abbiamo visto la decrescita esponenziale, verso l’infinitamente piccolo ...

Viceversa...

Osservate l’immagine sotto.

Ancora dividendo l’angolo giro in 6 parti uguali, in angoli cioè di 60°, Si parte dal segmento AB

e si costruisce BC ⊥ (perpendicolare) AB;

si ha: AC = 2 AB; (angolo BAC = 60°)

si continua costruendo CD ⊥ AC;

si ha: AD = 4 AB; (angolo BAD = 120°)

e ancora:

DE ⊥ AD; si ha: AE = 8 AB; (angolo BAE= 180°)

e così di seguito.

Si può ben dire: verso l’infinitamente grande!

Si ha in questo caso una progressione geometrica di ragione 2. La progressione geometrica delle potenze di 2, che abbiamo visto nell’esempio.

E ancora, se

in generale  x = n° angoli e y = distanza da A,

si ha: y = 2^x

E’ la legge dell’accrescimento esponenziale, rappresentata sul piano cartesiano dal grafico qui sotto

Anche stavolta grafici ben diversi  per la stessa legge!

Ora clic per aprire l’applet geogebra.

   Possiamo costruire una spirale equiangolare anche partendo da un angolo più piccolo, per esempio da un angolo di 30°, suddividendo cioè l’angolo giro in 12 parti uguali.

Per il momento (riferito a quando ci lavoreremo su!) osservate l’immagine, più avanti potremo comprendere meglio la progressione geometrica che ritroviamo in questa spirale (di ragione (radice quadrata di 3 )/ 2):

 

Ma attenzione: questa spirale non è da confondere con quest’altra!

Eh, non vi avevo detto che avremmo confrontato diverse spirali?

La spirale equiangolare ha affascinato i più grandi scienziati del 1600: Cartesio (quello del sistema di riferimento cartesiano!), Galileo, Torricelli.

Il matematico svizzero Jakob Bernoulli (1654 – 1705) definì la curva “Spira mirabilis”, la spirale meravigliosa, disponendo che essa fosse scolpita sulla sua tomba, a Basilea, accanto alla frase “Eadem mutata resurgo”, ovvero “sebbene diversa, rinasco identica”. In onore al matematico la curva viene anche chiamata di Bernoulli.

Per quanto riguarda la pietra tombale sfortunatamente lo scultore sbagliò: incise una spirale uniforme, quella di Archimede!

E ... con le spirali equiangolari non è mica finita. Ci sarà pure una sorpresa!

Ah, le ritroviamo spesso in natura!

Guardate anche QUI le immagini ...

Queste attività sono sempre tratte da

Matematica nella Realtà

E. Castelnuovo, M. Barra

La spirale equiangolare

Ragazzi,

Avevo detto che avremmo confrontato curve spirali diverse.

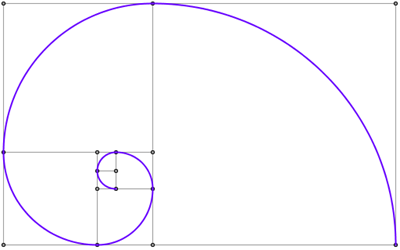
La spirale di Archimede, ricordate (o ri-vedete), è ottenuta tracciando delle circonferenze in modo continuo, aumentando il raggio in modo proporzionale all'angolo percorso.

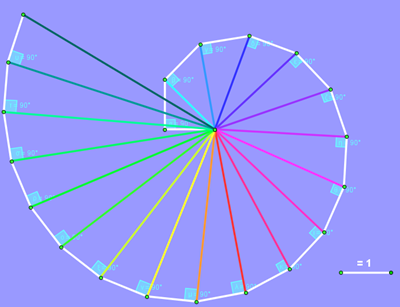
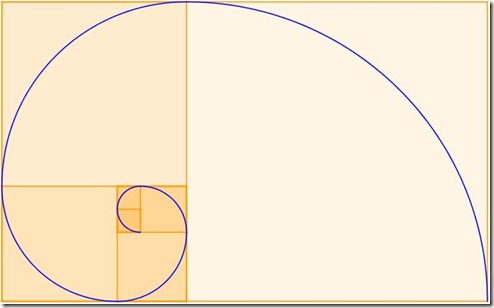
Un altro tipo di spirale può ottenersi dividendo l’angolo giro in 6 parti uguali, in angoli cioè di 60°. Osservate l’immagine (più sotto, ci sarà il link per l’applet):

Si parte dal segmento AB

e si costruisce BC ⊥ (perpendicolare) AC;

si ha: AC = 1/2 AB; (angolo BAC = 60°)

si continua costruendo CD ⊥ AD;

si ha: AD = 1/4 AB; (angolo BAD = 120°)

e ancora:

DE ⊥ AE; si ha: AE = 1/8 AB; (angolo BAE= 180°)

e così di seguito.

Si può ben dire: verso l’infinitamente piccolo!

In matematica si dice che si ha una progressione geometrica di ragione 1/2. [Qui sul blog abbiamo visto le progressioni aritmetiche, nelle quali la differenza fra qualsiasi termine ed il suo precedente è costante].

Si dice progressione geometrica (o per quoziente) una successione di numeri in cui è costante il quoziente fra un qualunque numero e il suo precedente.

Quindi, a partire da un termine iniziale (diverso da zero), ogni altro termine si ottiene moltiplicando il precedente sempre per uno stesso numero diverso da zero. Tale numero è detto ragione della progressione.

Es:

- La progressione geometrica delle potenze di 2:

1, 2, 4, 8, 16, 32, 64, 128, 256, 512, … ha termine iniziale 1 e ragione 2.

- La progressione geometrica delle potenze di 3:

1, 3, 9, 27, 81, 243, 729, 2187, 6561, … ha termine iniziale 1 e ragione 3.

- La progressione geometrica delle potenze di 1/2:

1, 1/2, 1/4, 1/8, 1/16, 1/32, 1/64, 1/128, 1/256, ... ha termine iniziale 1 e ragione 1/2.

Quest’ultimo esempio è quello che si presenta nella nostra costruzione della spirale:

la lunghezza dei segmenti, a seconda dell’angolo descritto a partire da AB, in senso antiorario, varia via via in ragione di 1/2.

In generale se  x = n° angoli e y = distanza da A,

si ha: y = 1/2^x

E’ la legge della decrescita esponenziale, rappresentata sul piano cartesiano dal grafico:

Ancora una volta due grafici tanto diversi rappresentano la stessa legge!

Ora, per aprire l’applet geogebra, clic qui.

   Al prox post: verso l’infinitamente grande...

Spirale uniforme o di Archimede [Aggiornato]

Eh, dopo lo zufolo...
ancora Archimede!
Eccome no. Uno dei primi matematici a studiare le proprietà delle curve a spirale, Archimede dedica un’intera sua opera, Sulle spirali, alla curva che prenderà il suo nome.
Per cominciare, ragazzi, andate a guardare quest’animazione. Clic sull’immagine
Piaciuta? :)
Noi possiamo immaginare uno spago che si srotola: per ogni 1/16 di giro si srotola di 1 cm. Cioè:
dopo 1/16 di giro lo spago è di 1 cm;
dopo 2/16 di giro lo spago è di 2 cm;
dopo 3/16 di giro lo spago è di 3 cm; ecc...
La spirale è uniforme, cioè cresce uniformemente, ossia il “passo” è sempre lo stesso.
Guardate l’immagine sotto, realizzata con GeoGebra.
Vedete l’angolo giro suddiviso in 16 parti;
all’angolo pari a 1/16 di angolo giro, corrisponde una circonferenza di raggio 1;
all’angolo pari a 2/16 di angolo giro corrisponde una circonferenza di raggio 2:
e così via.
Si segnano via via i punti di intersezione tra ciascuna circonferenza e la semiretta uscente dal centro A, lato del relativo angolo. Cioè: il primo punto, D, è l’intersezione tra la circonferenza di raggio 1 e la semiretta lato dell’angolo di ampiezza 1/16 di 360°; il secondo punto è l’intersezione tra la circonferenza di raggio 2 e la semiretta lato dell’angolo ampio 2/16 di 360°, e così di seguito.
Unendo successivamente tutti i punti si ottiene la spirale di Archimede (lo spago che si srotola).
Clic sull’immagine per aprire l’applet sulla quale potrete seguire la costruzione

Ogni punto è caratterizzato da due numeri:
D(1; 1/16), E(2; 2/16), F(3; 3/16), ecc....
Se indichiamo con y il numero degli angoli e con x la distanza del punto da A, il raggio dei cerchi, si ha sempre:
y = 1/16 x
Questa è l’equazione della nostra spirale.
Sul piano cartesiano è rappresentata da una retta per l’origine degli assi


 Spirale e retta hanno la stessa equazione nei due sistemi di riferimento. Due grafici tanto diversi rappresentano la stessa legge...

Attività tratta da Matematica nella Realtà

E. Castelnuovo, M. Barra

Abbiamo visto (con i compagni che vi hanno preceduto) e vedremo altre curve spirali, potremo fare dei confronti...

[Aggiornamento per i ''più grandi'']
A Questa Pagina approfondimenti dal punto di vista matematico, esempi animati e interattivi con possibilità di variazione dei parametri dell'equazione.  

Spirale degli irrazionali o di Teodoro e ...

Ragazzi, ricordate la "chiocciola delle radici quadrate"?
Ho rinfrescato la versione con geogebra

Clic sull'immagine per vedere animata la Spirale delle radici quadrate o degli irrazionali, detta anche Spirale di Teodoro di Cirene.
Aggiungiamo un esercizio, un'attività:
come "costruire" un segmento lungo: radice quadrata di un numero qualsiasi?
Dobbiamo necessariamente partire dal triangolo rettangolo di cateti unitari (di misura 1) ? Non è necessario.
Osservate la radice quadrata di 11:
si ottiene dal triangolo rettangolo di cateti: radice quadrata di 10 e 1;
la radice di 10 a sua volta dal triangolo rettangolo di cateti: radice di 9, cioè 3, e 1.
Questo ci suggerisce quindi che: basta partire dal quadrato perfetto che immediatamente precede la radice quadrata che si vuol costruire.
Facciamo un esempio su come fare con geogebra.
Costruzione del segmento lungo: radice quadrata di 18:
1) Con lo strumento: Segmento di data lunghezza, costruite il segmento AB lungo: 4 (radice di 16)
2) Costruite la circonferenza di centro A e raggio: 1
3) tracciate la perpendicolare ad AB passante per A
4) individuate il punto di intersezione tra la perpendicolare e la circonferenza
5) unite con un segmento tale punto (D) con il punto B ( segmento DB): avete costruito il segmento lungo: radice di 17
6) costruite la circonferenza di centro D e raggio: 1
7) tracciate la perpendicolare a DB passante per D
8) individuate il punto di intersezione tra questa perpendicolare e la circonferenza
9) unite con un segmento tale punto (E) con il punto B (segmento EB): avete costruito il segmento lungo radice quadrata di 18.
Noterete, vedi punti 2, 3, 4, 5, e punti 6, 7, 8, 9, che si tratta di ripetere la stessa procedura (si dice reiterare) per tutti i numeri irrazionali, le radici quadrate, che si vogliano costruire [si utilizza ripetutamente il Teorema di Pitagora .... vedi nostro post su citato).