Per la seconda
Ragazzi,
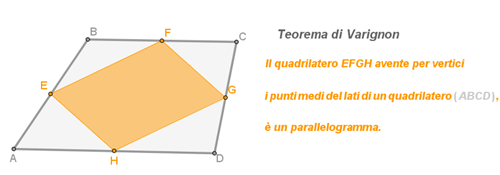
verificate con GeoGebra che vale il
Teorema di Varignon:
in un quadrilatero ABCD se E, F, G e H sono i punti medi rispettivamente dei lati AB, BC, CD e DA, allora EFGH è un parallelogramma.
Verificate facilmente che il teorema è valido anche per quadrilateri concavi.
E, attività più ... come diciamo noi?, dignitosa :
sapreste dimostrare perché il teorema è valido?
Vi aiuto:
per la dimostrazione dovete utilizzare questa
Applicazione del Teorema di Talete ai triangoli
Suu, molto interessante, con Geogebra facilissimo !
Clic sulla figura per aprire applet (troverete visualizzato un elemento di aiuto!)
Pierre Varignon (Caen, 1654 – Parigi, 23 dicembre 1722) è stato un matematico francese ...
Il teorema di cui parliamo fa parte dei teoremi elementari della geometria euclidea. Fu pubblicato negli Elemens de Mathematique nel 1731 (quindi dopo la morte del matematico).



















Vuoi vedere che adesso cominci anche a postare cose che non so!!! Bello questo teorema, anche senza Geogebra...che però lo rende indubbiamente più intrigante da guardare, ci si può muovere quanto si vuole ma i parallelismi non si spostano di nezzo grado :-) Brava la vostra prof, vero ragazzi? :-)
RispondiEliminaBellino vero, Nico? :-)
RispondiEliminasì, geogebra serve proprio a quello: mostrare la variante e l'invariante.
...faccio leggere il tuo commento a quei monelli là! :D :D