Operiamo con le radici quadrate

Scrivono M. Chiara, Giada e Letizia

Partendo dalla proprietà distributiva della radice quadrata:

$\sqrt{ 36 * 25 } \,=\, \sqrt{ 36 } * \sqrt{ 25 } \,=6 * 5$

e in generale:

$\sqrt{ a * b } \,=\, \sqrt{ a } * \sqrt{ b }$

e utilizzando la scomposizione in fattori primi per estrarre la radice quadrata di un numero (che ci serve anche per riconoscere se un numero è un quadrato perfetto: se tutti i fattori hanno l’esponente pari),

abbiamo imparato a calcolare le radici quadrate in un modo speciale. La prof ha detto che stavamo operando con le radici un po’ come faremo alle superiori!

Facciamo un piccolo esempio:

$\sqrt{ 20 } \,=\, \sqrt{4 } * \sqrt{ 5 }$

il numero 20 lo abbiamo considerato come 4*5 e poi applicata la distributiva.

La $\sqrt{ 4 }$  la mettiamo in questa forma:

$ \sqrt{ 2^2 } $

quindi:

$\sqrt{ 20 } \,=\, \sqrt{ 2^2 } *\sqrt{ 5 }$

Arrivati a questo punto abbiamo pensato che l’indice della radice(2) poteva essere semplificato con l'esponente di 2 (2):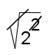 Abbiamo pensato bene ovviamente (avete messo la faccina, ma in ogni caso, o che modeste!), quindi:

$\sqrt{ 20 } \,=\,2 * \sqrt{ 5 }$

La $\sqrt{ 5 }$ è un numero irrazionale che possiamo lasciare indicato, non calcolato.

Abbiamo fatto poi altri esempi, con il radicando scomposto direttamente in fattori primi e poi opportunamente “scomponendo” se l’esponente era dispari. Es:

$ \sqrt{32 }\, =\, \sqrt{ 2^5 } \, =\, \sqrt{ 2^4*2 }\,=\, \sqrt{ 2^4 }* \sqrt{ 2 } \,=\,2^2* \sqrt{ 2 }\,=\,4* \sqrt{ 2 } $

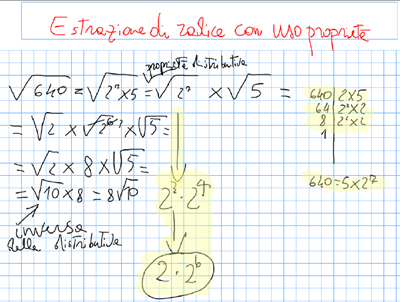
Ecco un altro esempio in figura:

Ragazzi, vedete? Abbiamo salvato solo la prima pagina del file LIM . Mi ritrovo solo questa Peccato, i bei colori di Veronica e Francesco! – Non mi fiderò più dei vostri suggerimenti!

Articoli correlati per categorie