Ragazzi,
I: dapprima, come d’accordo, dovete lavorare su... post sotto! Se poi volete, non è vietato cimentarsi su questo rompicapo ?
II: ecco a voi!
La bandiera del Castello
Il signor Sarto deve fare una bandiera quadrata proprio uguale a quella grandissima che sventola sulla torre più alta del castello. Ritrova un foglietto dove aveva disegnato il modello della bandiera, 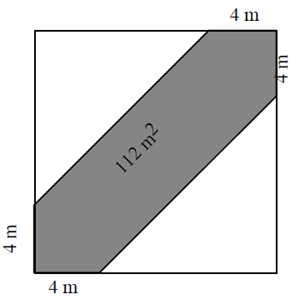
Quanto misura il lato della bandiera?
Spiegate come può fare il signor Sarto per essere sicuro di non sbagliare.
10° Rally Matematico Transalpino ( anno 2002)
Come commentato... potete lavorare sfruttando:
- relazione lato - diagonale di un quadrato e relazione inversa [vi ricordo che sapete lavorare con le radici anche indicando il n° irrazionale, senza calcolarne il valore decimale ...]
- oppure lavorare per via “geometrica” ... equi scomponibilità!
(quest’ultima via potrebbe essere utilizzata dai ragazzi della classe prima)
Aggiorno
Letizia e Maria Chiara (cl.II) hanno risolto il problema utilizzando la relazione diagonale-lato quadrato e hanno saputo eseguire passaggi matematici con le radici ....
In classe abbiamo risolto anche con il metodo di equiscomposizione.
Le ragazze hanno riportato le soluzioni su un foglio GeoGebra.
Ormai sono brave con slider e “condizioni per mostrare oggetto”, ma devo dire che mi diventano brave anche con il LaTex! Sono proprio contenta!
Clic su immagine (scelta apposta...)
- Anche in prima stamane abbiamo lavorato su questo problema: direi che sono stati bravissimi!
Giustamente, lo dicevano in un commento, “ho trovato un metodo ma ... non è da prima media” !
Infatti ragionavano sulla diagonale di un quadrato ... Non sapevano perciò andare avanti con le formule ma: hanno utilizzato le lettere per indicare i segmenti e hanno risolto il problema!
Abbiamo poi ricostruito la situazione con le striscioline e i fermacampioni e con l'equi scomposizione, facendo scorrere le figure... : bravi e partecipi tutti! Nonostante non tutte le porzioni di piano fossero “trascinabili”, mi sono piaciuti, in particolare, nel cogliere la diversa distribuzione di aree in una medesima figura.
Abbiamo avuto occasione di parlare di equivalenza, congruenza, e di tanto altro!
Raga... come d’accordo, io aspetto i disegni! (con le riflessioni... formule, ecc.)
Ecco risposta di Bea!
Ora, o voialtri... : altro metodo!
Ecco la seconda soluzione illustrata da Davì e Davide P.

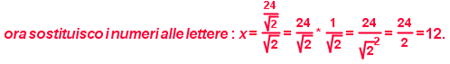



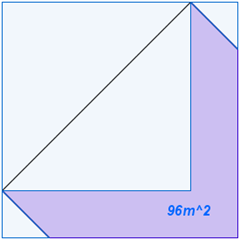



















Prof. un metodo l'ho trovato... ma non è da prima media e infatti non riesco ad andare a fondo, ma oltre a quello non ne trovo altri.
RispondiEliminaSte' :-)
RispondiEliminae vabbè, domani mi dici questo metodo "non da prima media" !
Domani mettiamo quindi la soluzione dei ragazzi di seconda.