Continuiamo a parlare di Q!

Maria Chiara si gode davvero lo sviluppo del tema! :-)

E ci dice...

Sviluppando il discorso sull’insieme Q, abbiamo scoperto cose nuove e meravigliose [che esagerata :-)]. Ora racconto com’è andata.

Antonello, nella sua relazione, ha voluto sottolineare il fatto che N è sottoinsieme di Q,

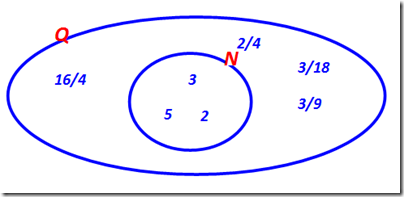
nel suo insieme scriveva come vedete, frazioni come 16/4, 2/4, 3/18, 3/9, ecc.. La professoressa, osservandolo ha notato le frazioni e ha detto: “Scusate ragazzi ma anche voi avreste scritto 16/4, 2/4, 3 /18 ecc..?”.

Pier Paolo ha parlato pronunciando un no secco [e te pare, Pier Paolo! :-)] e poi ha detto, “io per esempio avrei scritto 1/3 anziché 3/9, e poi al posto di 2/4, 1/2 e via dicendo”, infatti, era proprio la risposta esatta perché, ci ha ripetuto la prof, sono queste le frazioni “rappresentanti” la classe di equivalenza, cioè il numero razionale.

Tanto che, come si chiamano frazioni come 1/6, 1/3, 7/2, 11/18 ? Sono chiamate tutte frazioni primitive. Abbiamo scoperto anche quando una frazione è primitiva: quando il numeratore e il denominatore sono primi fra loro (quando non hanno più fattori in comune) . E…. visto come si collegano i vari argomenti? “Primi fra loro”, un concetto incontrato nella divisibilità.

Così, rispettando questa regola, abbiamo iniziato a elencarne molte, per esempio: 8/7, 7/6, e anche 220/19, 345/2, 99/20.

A sentire ciò, la professoressa è rimasta un po’ stupita e ha esclamato: “stranamente siete portati a fare degli esempi… con una caratteristica comune, a me ne sarebbero venuti altri …” Beh! Si può vedere anche dagli esempi elencati: tendiamo a mettere il numeratore più grande del denominatore.

Come mai?, ci chiedeva la prof. Gabriele ha detto che forse, dato che la frazione è una divisione, siamo abituati, in genere, al dividendo più grande del divisore, quindi… La prof ha detto che certamente, poteva essere un buon motivo.

La prof ci ha chiesto che cos’era per noi la frazione. Cosa voleva dire “frazionare”. Abbiamo detto che significava dividere (l’intero).

E quindi dividendo cosa ottengo, rispetto all’intero?

Delle parti più piccole, delle parti dell’intero!

Così ci ha indicato:

rappresentate i 6/5 di un nastro.

Ecco: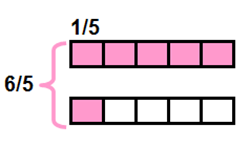

 devo prendere più dell’ intero! Non è bastato solo un nastro per prendere le sei parti dovute, quindi devo prendere l’intero più un altro quinto.

Mentre se noi prendiamo i ¾

Abbiamo preso una parte, una frazione dell’intero.

Quindi 3/4 , come 2/3, 5/8, ecc… sono vere frazioni!

   E ora arriva la parte più simpatica: non riuscivamo ad indovinare che nome dare alle frazioni ¾, ½ ecc.., quelle “una parte dell’intero”, e la professoressa che ci dava degli indizi per arrivarci: “ma scusate, che nome gli sta bene se queste frazioni sono veramente una parte dell’intero….” e ad un certo punto, Letizia interviene dicendo proprie! Immaginate che la professoressa dalla soddisfazione per essere arrivati alla risposta giusta, ha dato parecchie sculacciate a Letizia (naturalmente piano e scherzando) [per la verità la prof gliele ha date perché l’avevano fatta penare… :-)] poi se quelle erano proprie, i 6/5 ecc… erano improprie e le altre, come 10/5, 16/4, ecc... prima che finisse l’ora, siamo riusciti a dire che si chiamano apparenti (il termine esatto lo ha detto Giada)

Brava Maria Chia’! :-)

Articoli correlati per categorie