“Racconti” dalla I

Hanno detto i ragazzi di prima:

  noi apriamo il nuovo ... centinaio!

- Bravi!

Ed ecco i vostri lavori.

Cominciamo con Marco D.

A Marco è stato regalato un bel libro di Matematica divertente. Infatti è intitolato proprio Il Matematico si diverte e l’autore è Federico Peiretti.

Il primo capitolo del libro narra di Divertimenti matematici nell’antico Egitto.

In questo periodo parliamo di frazioni, Marco si è quindi soffermato su “Le frazioni nell’antico Egitto”. E vuole raccontare ai compagni:

Le frazioni dell’occhio di Horus

L’ idea di frazione per gli Egizi era molto primitiva, infatti conoscevano soltanto le unità frazionarie. Usavano un geroglifico che significava “parte”, e prendeva il ruolo del numeratore, per esempio 1/5 si scriveva così: , 1/3 così:

L’unica differenza era nella frazione 2/3 , per la quale si usava un simbolo specifico:

All’origine delle frazioni dell’antico Egitto c’è una leggenda. La leggenda narra che Horus figlio di Osiride e Iside, volle vendicarsi contro Seth il quale uccise il padre. Nella lotta Horus perse un occhio nel Nilo. Toth, il dio della giustizia, lo raccolse e lo ricompose.

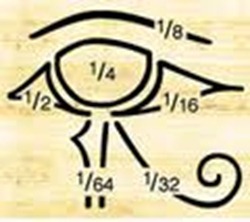
L’ occhio di Horus per gli Egizi ha un significato magico-religioso, lo usavano per siglare i documenti, e le sue parti assunsero un significato molto importante. Vennero adottate come frazioni dell’unità di misura della quantità di cereali, grano, orzo che veniva assegnata ad ogni famiglia. Ecco l’immagine dell’occhio:

Se sommiamo tutte le frazioni otteniamo 63/64, quindi manca 1/64 per arrivare all’intero. Si narra che Toth non riuscì a ritrovare la parte, ma la ricreò e la donò a Horus perché potesse completare il suo occhio divino.

Gli egizi come abbiamo detto prima, usavano soltanto le unità frazionarie ogni altra frazione era composta da unità frazionarie.

Un esempio l’abbiamo nel papiro di Rhind dove viene riportata una tabella di scomposizione di 2/n e di n/10 in unità frazionarie. Ad esempio:

9/10 = 1/30+1/5+2/3 [il libro riporta così ma, Marco, anche: 1/2 + 1/3 + 1/15, che sono tutte unità frazionarie]

2/7 = 1/28+1/4

Ora, ragazzi, provate voi a scomporre in unità frazionarie (vi aiuto):

2/5 = ...  + ...

3/4 = ... + ...

5/7 = ... + ... + ...

E ancora un aiuto: ricordate la proposta di soluzione del problema della suddivisione dei 3 appezzamenti di terreno fra 4 figli .... ?  Qualcuno di voi ha detto: divido due terreni a metà e ne do una parte a ciascun figlio, l’altro terreno .... Ecco: avremmo usato le frazioni egiziane!

  - E ora, torniamo ai tempi moderni con ... Geogebra!

Davì ha costruito correttamente il rombo. Tanto che, orgogliosamente lo chiama rombo indeformabile. Clic su immagine, dal file di Davì, per vederlo.

Beatrice invece mi ha detto di essere andata a curiosare sul blog del prof Daniele e di aver visto un’altra dimostrazione dell’area del trapezio. [ecco che mi combinano i miei ragazzi, prima di cliccare sui link del nostro blog .... Scherzo. Al contrario, mi fa piacere che vadano ad esplorare in rete!]

Ed ecco che Bea dice e fa:

Dimostrazione dell'area del trapezio

Sappiamo che la caratteristica principale del trapezio è di avere 2 lati paralleli (B (base maggiore), b (base minore)).

Gli altri 2 sono i lati obliqui, non paralleli.

La distanza fra le 2 basi si chiama altezza (h).

Trasformando il trapezio mediante l'equiscomposizione/composizione in un triangolo, cioè unendo la base minore a quella maggiore e unendo i loro vertici,

Clic su figura - Mi accorgo ora che Bea scrive nel foglio di lavoro: Muovendo i vertici l'area e i segmenti CD e BE non cambiano! Io so che intendeva, e ne era felice, che la costruzione non si deforma, conserva le proprietà.

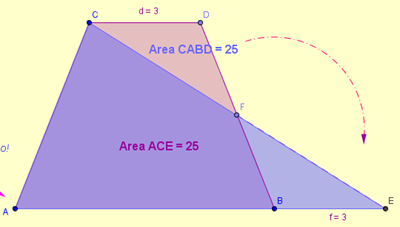
ci trasportiamo automaticamente un triangolo ottusangolo con un lato uguale alla base minore del trapezio (in poche parole lo abbiamo “tagliato”dal trapezio e aggiunto alla base maggiore) notiamo che le due figure ABDC e ACE sono equivalenti.

Possiamo dire allora che l'area del trapezio è (B+b)*h/2, e che è equivalente a quella del triangolo che ha per base la somma delle basi del trapezio e come altezza la stessa altezza del trapezio.

(Prof, ma i triangoli si trovano in ogni figura!! – mi scrive Bea. Già, ne abbiamo poi parlato ...)

Bea, ragazzi, come vi ho detto, dobbiamo però dimostrare che il triangolo trasportato automaticamente, “tagliato”dal trapezio è equivalente al triangolo FBE. Ma prima dobbiamo scoprire altre proprietà sulle rette che si incontrano ...

Ragazzi: lode anche a voi!

Articoli correlati per categorie