Home page * GeoGebra * Excel * Matematica nella Storia. I Grandi Matematici * Matematica ricreativa * Libri * Le Curve Celebri * Immagini per la Matematica * Tutoriali * Le Formule più belle * Matematica e ... *
Altri modi per visualizzare il blog
INFORMATIVA SULLA PRIVACY E SUI COOKIE
*MATERIALE DIDATTICO *Risorse didattiche e SCUOLA *BLOG DIDATTICI e colleghicheleggo *Risorse EXCEL - OFFICE *Info CREARE e ARRICCHIRE IL PROPRIO BLOG *Altro Blogroll *Condivisioni *Visualizzazione formule matematiche
Ragazzi (II)
come promesso 
un bel quesito.
Triangolo EFG
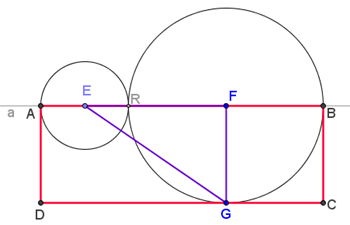
In figura E e F sono i centri di due circonferenze tangenti esternamente, in R, e la retta a taglia le due circonferenze in A e B.
ABCD è un rettangolo di area pari a 15.
Quanto vale l'area del triangolo EFG?
da Kangourou - Categoria Cadet 2002
Buona risoluzione! Se volete, si può discutere qualche dubbio in commenti.
Etichette: Giochi, matematica ricreativa
I vostri commenti sono graditissimi, l'interazione è molto utile!
Non ci piace però comunicare con "anonimi". Vi preghiamo di firmare i vostri messaggi.
Come fare:
Cliccare su Nome/URL.
Inserire il vostro nickname nel campo "nome".
Lasciate vuoto il campo URL se non avete un blog/sito.
Grazie!
Post
Buonasera ho provato a risolverlo
RispondiEliminaconsiderando che il quadrato BCGF
fosse un terzo del rettangolo grande, mi sono ricavato l'altezza del rettanolo che uguale al raggio
della circonferenza grande ed il diametro della piccola.
Dopo dei passaggi matematici sono arrivato alla conclusione che l'area
è di 3,75 cm^2.
Gabri,
RispondiEliminammm, forse la figura trae in inganno ma non possiamo dedurre "ad occhio" che il quadrato BCGF
sia un terzo del rettangolo grande.
Non è corretto.
L'unica cosa che posso dirti è che è corretto il tuo risultato.
... ma ... non vale così! :-)
Anzi, ti dico anche: non occorre proprio calcolare basi e altezze.
Piuttosto solo "confronti" basi-altezze!
L'area del triangolo è esattamente un quarto dell'area del rettangolo quindi 3,75 cmq; quanto perchè, mentre un cateto è uguale al lato corto del rettangolo, l'altro cateto è uguale alla metà del lato lungo del rettangolo quindi l'area del triangolo ( metà del prodotto dei cateti ) risulta un quarto dell'area del rettangolo ( cateto X doppio dell'altro cateto )
RispondiEliminaCorrado
Ciao Corrado,
RispondiEliminabravissimo :-)
sì, in classe anche noi avevamo risolto con le medesime osservazioni.
grazie per il commento!