Relazione di Marco N.
Nel nostro libro di testo c’è un’attività:
formule che portano a ottenere numeri primi.
Abbiamo verificato con Excel una formula scoperta da un matematico francese del 1600, Pierre Fermat.
In un’opera, Varia opera Mathematica, aveva fatto l’ipotesi che tutti i numeri che si ottenevano con la formula:
$2^{2^{n}}+1$
dovevano essere per forza numeri primi.
E così lo eseguo su Excel:
Scrivo sulla casella A1: n (che sta per numero) e da A2 a A5 i numeri da 1 a 4
In B1 scriviamo: formule; nella casella B2 questa formula:
=2^(2^A2)+1 .
Poi clicchiamo sopra, e teniamo premuto il tasto sinistro e trasciniamo fino alla casella B5
In questo modo otteniamo numeri primi.
Secondo Fermat, con questa formula si ottenevano sempre numeri primi.
Più tardi, nel 1732, un altro grande matematico, lo svizzero Leonardo Eulero nel libro Opuscula Analytica smentisce e afferma che:
$2^{2^{5}}+1$
non è un numero primo!
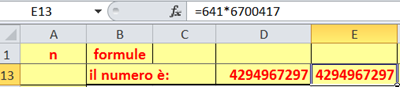
Infatti questo numero è il prodotto di: 641*6.700.417
Tutto questo lo verifico con Excel, scrivendo 5 nella casella A6 e trascinando la formula in B6.
I primi 4 numeri ottenuti sono primi, l’ultimo non è primo.
Bene, Marco. Non hai poi verificato che l’ultimo numero è il prodotto di: 641*6.700.417. Guarda la formula in cella E13 e il risultato.



















Nessun commento:
Posta un commento
I vostri commenti sono graditissimi, l'interazione è molto utile!
Non ci piace però comunicare con "anonimi". Vi preghiamo di firmare i vostri messaggi.
Come fare:
Cliccare su Nome/URL.
Inserire il vostro nickname nel campo "nome".
Lasciate vuoto il campo URL se non avete un blog/sito.
Grazie!