Siamo ripartiti!

Ragazzi,

nell’attesa dei vostri “racconti”, intesi come lavori, scoperte, creazioni ... ,

può esservi comodo, e anche per comunicarlo ai genitori, un riepilogo della nostra prima giornata di lezione, dopo quella del benritrovati!

    In entrambe le classi, II e III sez A, dopo esserci scambiati propositi, progetti, aspirazioni (ho ascoltato davvero dei bei “progetti”) , aver ricordato regole e stipulato patti (che sarà necessario, ogni tanto, rinfrescare...), aver sottolineato la straordinarietà di ciascuno di noi, che a volte un po’ più difficilmente affiora, perciò ripromessi di aiutarci l’un l’altro perché ciò avvenga,

siamo ripartiti con le nostre attività!

In II:

Ci si proponeva per domani (libro di testo!) la ripresa del calcolo con le frazioni. Però: con le frazioni. Ma con i numeri razionali!

  Si ... qualcuno dei ragazzi ha visto la mappa, pubblicata recentemente.

Quindi, la classe è ora più o diversamente eterogenea rispetto all’anno scorso, siamo ripartiti dall’esigenza di ampliamento dell’insieme N dei numeri naturali: per via di quelle divisioni non fattibili in N.

  Abbiamo ricordato: perché razionali? Origine del termine razionali: dal latino ratio come, abbiamo faticato un po’ ma ce l’abbiamo fatta, ragione, nel senso di rapporto, quoziente.

E ancora, infatti: l’insieme dei razionali viene indicato con  la Q maiuscola. Q sta per quoziente!

E poi abbiamo disegnato:

  che è un diagramma di Eulero-Venn e i signori Eulero e Venn non si sono neppure mai incontrati ... (vi invito a leggere QUESTO, ragazzi)

e abbiamo messo dentro: 2/3, 3/4, 18/8 (oppure 9/4 che è primitiva. “Sì sì, sono equivalenti, per l’invariantiva...”), ecc...

Ma abbiamo potuto mettere anche: 5, 8, ..... perché 5 = 5/1 e “tutti i naturali il denominatore, sottinteso, lo hanno: è l’1”, ma anche: 5 = 10/2, 15/3, ecc ... (su questo torneremo ancora).

E allora: N è un sottoinsieme di Q, N è incluso in Q, N ⊂ Q [per il momento va bene così] e:

 così possiamo sistemare meglio i numeri razionali! E tutti, o quasi, hanno sistemato qualche numero ...

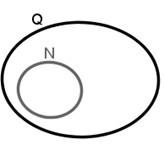
Sull’argomento, non vorrei ricordare male, non abbiamo detto altro...

Perché volevamo divertirci con il Triangolo!

E lo abbiamo fatto anche in III

Capita la costruzione, son già venute fuori delle belle cosette:

in III:

1) il triangolo è simmetrico (richiami su simmetria... per i nuovi! Bravi eh: hanno sistemato correttamente le dita della mia mano che si specchiava...!) rispetto a un asse che lo taglia centralmente (simmetria assiale)

2) la seconda diagonale è costituita dalla successione dei naturali

(in terza non abbiamo avuto altro tempo)

In II:

punto 2 precedente

3) Marco D. ha ritrovato i numeri triangolari

4) Giovanni ha cominciato a dire che: di riga in riga si moltiplica per due. Questa dobbiamo puntualizzarla...

5) Beatrice cominciava a vedere le potenze di 11

Fine dell’ora!

Io aspetto lavori che certifichino le scoperte!

Articoli correlati per categorie