Home page * GeoGebra * Excel * Matematica nella Storia. I Grandi Matematici * Matematica ricreativa * Libri * Le Curve Celebri * Immagini per la Matematica * Tutoriali * Le Formule più belle * Matematica e ... *
Altri modi per visualizzare il blog
INFORMATIVA SULLA PRIVACY E SUI COOKIE
*MATERIALE DIDATTICO *Risorse didattiche e SCUOLA *BLOG DIDATTICI e colleghicheleggo *Risorse EXCEL - OFFICE *Info CREARE e ARRICCHIRE IL PROPRIO BLOG *Altro Blogroll *Condivisioni *Visualizzazione formule matematiche
da qui.
Stavolta un po’ più impegnativo per noi [attenzione, le proprietà geometriche dobbiamo ritrovarle, sono più impegnativi i passaggi matematici]. Metto la soluzione, non prima di un aiuto, per provare a riflettere, per la discussione in classe, o per l’eventuale lettore che volesse risolvere da sé. Giusto per i ragazzi, i passaggi matematici sono forse sovrabbondanti...!
Clic su img
I vostri commenti sono graditissimi, l'interazione è molto utile!
Non ci piace però comunicare con "anonimi". Vi preghiamo di firmare i vostri messaggi.
Come fare:
Cliccare su Nome/URL.
Inserire il vostro nickname nel campo "nome".
Lasciate vuoto il campo URL se non avete un blog/sito.
Grazie!
Post
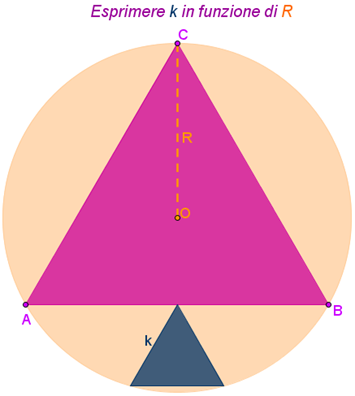
Molto molto carino questo problema, con la geometria analitica si fa presto eheh...ma ovviamente i tuoi ragazzi non l'hanno ancora studiata immagino! Forse però sanno di che si tratta! Bravissima Giò, come sempre
RispondiEliminaNico, sì più o meno i raga sanno già cos'è la geometria analitica
RispondiEliminaSoltanto ... l'hai visto, neppure io l'ho risolto con l'analitica. Ché, non potendola sfruttare "alle medie", mica la so applicare tanto! :-(
Se hai il tempo di darmi l'idea.... la soluzione analitica, grazie!!!
ihihih, ma rientra dalle ferie!:-)
Con piacere Giò. Parti sul piano cartesiano dalla circonferenza più semplice possibile, che abbia centro nel centro del piano cartesiano e raggio 1. Quindi C=(0,0) è il centro. L'equazione di questa circonferenza è molto semplice, e cioè x**2-y**2=0. Poi traccia una linea orizzontale sotto l'asse delle ascisse in modo da intersecare la circonferenza in due punti B e C. Tenendo conto delle proprietà del triangolo equilatero inscritto, imponi che i tre segmenti BC, AB e AC, dove A=(0,1) (cioè uno dei due punti dell'asse delle ordinate che interseca la circonferenza) siano uguali. A questo punto vieni a conoscere l'ordinata dei due punti B e C, che è ovviamente la stessa, e ricavi tranquillamente la misura richiesta.
RispondiEliminaChe bello che mi hai dato la possibilità di ripensare a cose ormai passate! Grazie amica mia, un abbraccio
ooh, Nico,
RispondiEliminati ho fatto lavorare! :-)
Bene! Così ricavo esattamente le misure dei segmenti richiesti. Io non mi ponevo questo obiettivo perché il problema chiede solamente la relazione tra k e R.
Comunque il tuo esempio mi è stato utile, non avevo pensato a questa soluzione.
grazieeee! Amico! :-)