Perché ogni scarabocchio ...

“è figlio di mamma Matematica”! 

Raga,

vi ho ricordato da poco l’affermazione fatta da un matematico, che, più o meno, suona così. Tant’è che ...

Di recente, nel corso di una riunione, mentre ascoltavo, come al solito scarabocchiavo. E fra i miei scarabocchi mi sono ritrovata un bel simbolo dell’infinito! Lo conoscete: ∞

Mi sono chiesta poi: ma ci sarà, quale sarà, la legge matematica che rende conto di questo simbolo? Cioè quella che si dice, in matematico, la sua equazione.

E certo, c’è! Non la sapevo ma non è stato difficile trovarla!

La seguente. E’ un po’ complicata per noi, ma è bello sapere:

(x²+y²)² = 2 a² (x² - y²)

E ... Geogebra mi disegnerà questo simbolo, o meglio, questa curva?

Come no! Sul campo di inserimento di Geogebra ho dovuto digitare così:

Curva[a sqrt(cos(2 α)) cos(α), a sqrt(cos(2 α)) sin(α), α, 0, 2 pi]

Bella no?

Oh, non spaventatevi, fra qualche anno appena, queste cose le saprete più di me! (ricordate? ve lo dico sempre!)

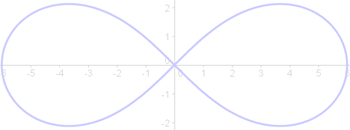
La curva matematica a forma di infinito ha un nome. Si chiama Lemniscata di Bernoulli.

Fu descritta per la prima volta nel 1694 da Jakob Bernoulli, un matematico e scienziato svizzero, dal quale prende il nome.  Bernoulli la chiamò lemniscus, che in latino significa ‘nastro annodato’: nell’antica Roma era un nastro pendente dalle corone.

Ed ecco il risultato con Geogebra. Clic! – Potete animare o muovere lo slider.

Maa...

più bello è vederla formarsi da una circonferenza come luogo!

Iperbole e circonferenza

• Si costruisce un’iperbole equilatera (in seconda sanno già l’equazione: x * y = k oppure y = k/x)
• poi una circonferenza di centro A, un punto dell’iperbole,
• passante per il centro dell'iperbole

Il luogo delle circonferenze al variare di A è una lemniscata di Bernoulli.

Guardate un po’. Cliic!

E non finisce qui. Si può costruire la lemniscata anche come luogo di punti. Lo vedete su un’altra applet. Clic

Articoli correlati per categorie