Ecco le soluzioni del
Due a settimana …_18
Quesito 1 - a, relazioni tra serie numeriche
Beh sì, estremamente semplice per invogliare tutti. Hanno risolto,
per la classe prima: Ludovica, Margherita, Antonio, Stefano P., Gabriella, Stefano B., Sofia, Andrea, Giorgia.
Per la classe seconda: Yuri, Davide, Nicol, Elena, Andrea, Sara, Maria, Paola, Marta C., Luca, Aurora, Roberta, Antonio, Valentina.
Inutile citare le singole risposte, possono così sintetizzarsi (dalle risposte più complete):
la relazione che lega la prima fila alla seconda è la differenza di 5.
Ma per trovare i due numeri mancanti non è sufficiente, dato che possono essere numeri qualsiasi [che abbiano per differenza 5]. Si nota la regolarità tra le due file: c'è sempre una differenza di 2 unità in ordine decrescente, quindi i numeri mancanti sono: 24 e 19.
Quesito 1 – b, relazione numerica appena più impegnativa:
Solutori per la classe prima: Ludovica, risultato corretto, spiegazione non troppo corretta, Sofia, Gabriella, Stefano B., Antonio, Stefano P., Andrea e Fabio.
Per la classe seconda: Yuri, Davide, Maria, Paola, Marta C., Luca, Roberta, Antonio, Valentina, Andrea, Elena.
La relazione come dire, più canonica, trovata dalla maggior parte dei solutori è la seguente (dalla risposta più sintetica):
La differenza tra il primo e il terzo numero di ogni terna, moltiplicata per 2 da il numero centrale, quindi il numero che completa la terza terna è 16.
Tralascio i vari “ho fatto: 20-14 e poi ho moltiplicato per 2, ecc …”
Paola invece, così ragiona:
Il numero mancante è 16 perché nella prima terna faccio: 20 - 12 = 8; 8 + 6 (cioè 12/2) = 14, nella seconda faccio 12 - 4 = 8; 8 + 2 (cioè 4/2) = 10. Quindi: il primo numero meno il secondo più la metà del secondo = il terzo numero. Nella terza terna mancava il 16 perché facendo 22 - 16 = 6; 6 + 8 (cioè 16/2) = 14.
E Andrea, così (ma direi che bara un po’ … !):
ho notato che in ogni terna la somma delle differenze è 16. Nella prima faccio: 20-12=8, 20-14=6 e 14-12=2; 8+6+2=16; nella seconda terna faccio 12-4=8, 12-10=2 e 10-4=6; 8+2+6 = 16; nella terza terna posso fare solo 22-14=8, quindi devo trovare un numero che sottratto al 22 dia 6 e che se gli viene sottratto 14 dia 2 e questo numero è 16. [a rigor di regolarità l’ultima sottrazione dovrebbe essere 14-16. Facciamo che Andrea considera il valore assoluto! ]
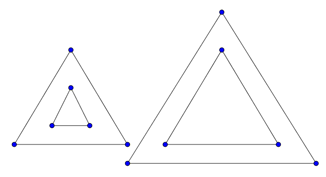
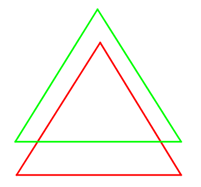
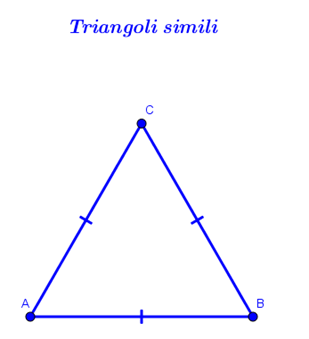
Quesito 2 – a, i triangoli …simili, a precisa distanza
Il quesito ha dato da pensare più di quanto prevedessi. Vero è che non si legge con attenzione, non si bada ai “connettivi logici”. E sì, la prof ha dovuto in più di un caso ricordare che due proposizioni legate dal connettivo e per corrispondere complessivamente a verità, devono verificarsi cioè essere vere entrambe. Cioè, entrambe le circostanze devono verificarsi! Già, queste cose abbiamo avuto modo di sottolinearle, in seconda ovviamente più che in prima, eppure l’indicazione: “in modo che ciascuno dei suoi lati sia parallelo ad un lato del triangolo iniziale e sia esattamente a 1 cm di distanza da esso” è stata quasi sempre disattesa nella seconda parte. Si dovrà insistere sulla logica, certo…
Ma veniamo ai solutori e alle soluzioni.
Per la classe prima
Stefano P., trova 5 soluzioni, disegni un po’…. insomma!
e poi invia foto, di costruzioni meno curate…
E secondo me non ha approfondito!
Gabriella trova le soluzioni:
E poi non fa opportuno sforzo…
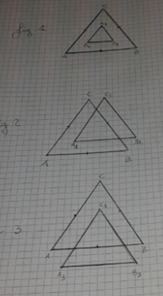
Antonio invia la foto di tre disegni…
Stefano B. :
Come sopra, uno sforzo in più no!
Ludovica trova una soluzione, disegno … insomma
e si avvicina con altre due. Orribile la seconda foto!
Fabio, insomma i disegni…
Per la classe seconda
Beh, godiamoci il lavoro di Roberta, la quale oltre a trovare tutte le soluzioni, realizza le precise costruzioni su Geogebra. Si può visualizzare l’applet al clic sull’immagine. Roberta dice:
Maurizio può disegnare il nuovo triangolo richiesto in 8 modi diversi.
Per trovare tutti i triangoli (presenti nel file GeoGebra) mi sono servita della similitudine dei triangoli, quindi triangoli ingranditi o rimpiccioliti ma con angoli corrispondenti congruenti e lati in proporzione.
Paola. Con il numero di disegni e le posizioni ci siamo, con le costruzioni un po’ meno…
Andrea. Come Paola
Maria, come Paola e Andrea..
Non si sprecano:
Davide:
Luca:
Antonio, non completo e disegni insomma!
Marta C.
E, pubblico/non pubblico l’orribile foto di Aurora? Sia!
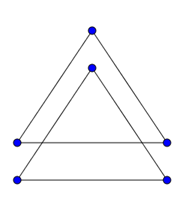
Quesito 2 – b triangoli...
I solutori della seconda: Andrea, Paola, Yuri, Luca, Aurora, Elena, Marta C., Roberta, Antonio, Maria.
In sintesi, dalle risposte meglio espresse, la soluzione:
L'ampiezza dell'angolo ABE è 40°: i triangoli ABC e CDE sono equilateri e congruenti e anche gli angoli sono uguali cioè di 60°; osservando la figura noto un altro triangolo, il triangolo BCE che ha un angolo formato dalla somma di 80°(angolo già citato nel testo) e 60°(angolo di un triangolo equilatero), quindi un angolo ottuso: 60° + 80° = 140°. Il triangolo BCE è isoscele, perché ha come lati uguali un lato di ogni triangolo equilatero congruente. Perciò gli angoli alla base di BCE sono uguali e hanno ampiezza di 20°: (180°-140°)/2. Quindi per trovare la misura dell'ampiezza dell'angolo ABE: 60° - 20° = 40°.
Bene, anche stavolta mi pare di aver concluso! Avvertitemi se qualcosa o qualcuno ho scordato… Ma in tempi regolamentari, non dopo un mese!
Solito BRAVO a chi ha lavorato, e anche a chi ha tentato …
Il prossimo appuntamento sarà come sempre, dal prof Davide.








































Lo sapevo, lo sapevo! Uff!
RispondiEliminaVedo qui una razione abbondante di soluzioni servite dalla prof. Io invece sono più in ritardo che mai. Ho a malapena impiattato il primo! Per il secondo devo ancora trovare il tempo per analizzare gli ingredienti. Ma adesso mi ci metto, eh!
Intanto aggiungo i miei complimenti a quelli della prof: per chi ha lavorato, per chi è riuscito e per chi ha tentato. Bravi!
E grazie alla prof!
Ci "vediamo" presto.
Ahah, la prof stavolta ha preparato e servito velocemente.
RispondiEliminaGrazie, tu fa pure con comodo, mi godrò le tue portate più elaborate :-)
A presto!