Suvvia,
stimolata dal post del prof.Davide,
vengo finalmente a confezionare il post delle nostre soluzioni del
Sarà mica matematica 45
Non so se lo farò in più tappe, un po’ di influenza, un po’ di farmaci, oh, mancavano solo questi a causare rallentamenti!
Comunque, cominciamo con il
Quesito 1, gli sviluppi di una piramide
Per la classe seconda, risolvono: Stefano P., Margherita, Fabio, Sofia, Gabriella, Andrea, Stefano B., Antonio.
Per la terza: Yuri, Andrea, Maria, Roberta, Paola, Aurora, Luca, Elena, Antonio, Davide, Sara.
Si sostiene che:
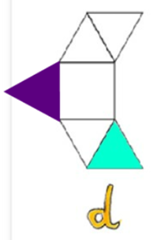
L'unica sagoma con cui non si riesce a formare una piramide è la 'd', perché se pieghiamo lungo le linee ci sono due facce che si sovrappongono: quelle non tangenti [qui è da tangere] ai lati della base quadrata.
In molti, soprattutto della seconda, costruiscono le piramidi con le sagome, bene. Vengono fornite varie immagini o foto. Pubblico parte di quanto arrivato via e mail, il cartaceo, eh no!
Luca:
Margherita, costruisce le sagome corrette e mostra le piramidi. Riporto un esempio:
Elena:
Il triangolo che non ci vuole è indicato con il color verde acqua, invece la parte viola indica dove dovrebbe stare. Le altre sagome sono corrette.
Infine Sofia, della seconda, (brava Sofi!, ha fatto tutto da sola: mi sono aiutata con un tutorial da Youtube) ci fa una sorpresina. Realizza la piramide in geogebra 3D, da uno degli sviluppi. Clic su immagine (peccato, sul foglio di lavoro dell’applet non sono riportati gli strumenti geogebra per poter ruotare a piacere la figura, ma si può sempre scaricare il file):
Quesito 2, rettangolo, area e perimetri…
Risolvono, per la seconda: Stefano P., Margherita, Fabio, Sofia, Gabriella, Andrea (ma non trova il perimetro maggiore), Stefano B., Antonio e Ludovica.
Per la terza: Yuri, Andrea, Maria, Roberta, Paola, Aurora, Luca, Elena (ma non trova il perimetro maggiore), Antonio, Davide, Sara.
Si spiega così:
le coppie [delle misure] dei lati del rettangolo di area 12 cmq, possono essere: 4 e 3, 12 e 1, 6 e 2 [in cm!]. Dovendo trovare il perimetro maggiore, ho fatto ( 2 X 12) + ( 2 X 1 ) = 26 [cm!]. , infatti usando le altre coppie ottengo perimetri più piccoli: 14 e 16.
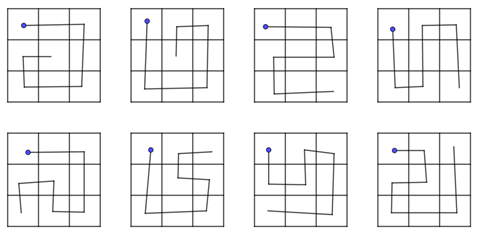
Quesito 3, scacchiera e pedina.
Ancora per la seconda: Stefano P., Margherita, Fabio, Sofia, Gabriella, Andrea, Stefano B., Antonio e Ludovica.
Qualche immagine:
Marghe,
Fabio
Trovano diverse soluzioni (7-8) anche Ludovica, Sofia, Stefano B. e Gabriella. Quest’ultima aggiunge sul file geogebra:
Ecco, a questo proposito, per la seconda parte del quesito, nessuno, neppure dalla terza, invia alcun tentativo di soluzione. Ci si limita ad affermare:
Per quanto riguarda la seconda parte trovare una soluzione è impossibile, perché o bisogna muoversi in diagonale o passare due volte in una casella; il tutto contro le regole.
E dunque, a questo proposito:
Perché non andare a leggere il post del prof. Davide e le risposte di alcuni ragazzi? Troverete perfino una bella sorpresa: si può!!!
Inoltre c’è la bella spiegazione del prof!
E per la classe terza risolvono: Yuri, Andrea, Maria, Roberta, Paola, Aurora, Luca, Elena, Davide, Sara, Antonio.
Un’immagine è sufficiente per tutte!
Quesito 4, lettera uguale cifra uguale.
Per la classe seconda: Stefano P., Margherita (ma non trova il valore più alto di OTTO) , Fabio, Sofia, Gabriella (neppure lei si da da fare per il valore più alto!), Stefano B., Antonio.
Ahi, mi accorgo che, insomma, le risposte più soddisfacenti (per un certo verso poiché non spiegano), sono solo quelle di Stefano B. e Antonio. Che consegnano il cartaceo ah!!
Il loro “SEI +TRE = NOVE”, risulta (o, ma entrambi stesse cifre? Dovrò sospettare?):
per cui OTTO = 7997
Stefano P. invece:
ho sostituito le lettere in questo modo:
infatti per ottenere come somma il numero più grande possibile ho dovuto sostituire le lettere s e t con le unità di valore più grande: 9 e 8. La i doveva essere per forza uno 0 perché sommata alla e dava come risultato e. Alla r ho dato valore 2. Il risultato che ho ottenuto è 1764. La scritta otto, quindi corrisponde al numero 7887. Ste’, capito? Ti bastava cambiare di posto le cifre 9 e 8.
Anche Fabio e Sofia, che si limitano a operare senza spiegare, compiono lo stesso errore (ehi, anche in questo caso, sono state usate le stesse cifre! Ma sì ma sì, sono certa sia una coincidenza):
Per la terza, risolvono bene, trovando il valore più alto per OTTO: Roberta, Andrea (che opera soltanto), Elena (pure!), Paola, Antonio, Yuri, Sara, Davide e Luca. Aurora non trova il valore più alto richiesto.
La risposta con la migliore spiegazione è quella di Roberta:
Basandomi sulla frase evidenziata: "A lettera uguale corrisponde cifra uguale"; ho attribuito ad ogni lettera una cifra.
I = 0 → perché I+E=E E-E=0 [!];
N = 1 → perché avendo un'addizione composta da due soli addendi e rispettando tutte le richieste, non ottengo resti, sommando quindi le due cifre maggiori S e T ottengo una decina;
T = 9 → perché devo attribuirgli un valore alto per andare a formare OTTO;
S = 8 → perché devo attribuirgli un valore alto dato che S+T=O che fa a formare OTTO;
O = 7 → come conseguenza di S+T;
V = 6 →↓
R = 4 →→
E = 2 →↑
L'operazione finale diventa: 8 2 0 + 9 4 2 = 1 7 6 2
OTTO = 7997
Bene, mi pare di aver concluso. Due sole tappe, due!
Se ho scordato qualcosa o qualcuno, avvertite!
Ovviamente, sempre BRAVO! a chi ha lavorato, a prescindere dai risultati ottenuti. Ognun sa che se ne terrà conto!
E come sempre, grazie, prof. Davide!
Alla prox. A energie ritrovate…!








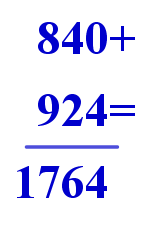





















Nessun commento:
Posta un commento
I vostri commenti sono graditissimi, l'interazione è molto utile!
Non ci piace però comunicare con "anonimi". Vi preghiamo di firmare i vostri messaggi.
Come fare:
Cliccare su Nome/URL.
Inserire il vostro nickname nel campo "nome".
Lasciate vuoto il campo URL se non avete un blog/sito.
Grazie!