Due a settimana …_19, le soluzioni

Sì, le soluzioni del

Due a settimana …_19

Stavolta siete riusciti a chiederle anche voi Oddio, qualcuno!

Eccole subito

Quesito 1 aritmetico

Solutori per la classe prima: Giorgia, Ludovica, Margherita, Gabriella, Antonio, Sofia, Stefano P., Stefano B.

Per la seconda: Yuri, Andrea, Paola, Davide, Elena, Elisa, Roberta, Aurora, Michele, Luca, Maria, Sara, Antonio, Valentina e Marta D.

Mi ritrovo la soluzione anche in un foglietto anonimo, non saprei a chi attribuire.

Tutti considerano che la cifra c debba essere uno 0 in quanto sommando le cifre del numero bc si ottiene il numero b (qualcuno, preciso: lo zero nell’addizione è neutro)

Per il resto in tanti ammettono vari tentativi, quale più ragionato quale meno.

Mi piacciono le soluzioni di:

 Sofia: sono partita risolvendo la C perché se B+C deve dare B sicuramente C sarà 0. Poi ho trovato la B, che deve essere una cifra pari; il 2 va bene, perché: A+B+A deve essere uguale a BC, provando A=9 nell'operazione A+B+A, A+B+A=9+2+9=BC=20 e B+C=2 e C=0.

Gabriella: ... poi ho cercato dei numeri a 3 cifre dove la somma mi dia un numero a 2 cifre con la seconda cifra che sia 0 è la prima b.
Con l'1 non è possibile, allora ho provato con il 2 al centro seguendo il suo aiuto, e ho trovato 929
9+2+9=20     aba
2+0=2       bc
2 = b
quindi a=9   b=2   c=0

Anche Michele ha provato prima con b=1 che “NO”, b=2 invece “OK”

Altri considerano che b = 2 perché attribuendo a b una cifra inferiore o maggiore di due, la cifra a diventa o un numero decimale o un numero a due cifre. Quindi: l’unica cifra che moltiplicata per 2 aggiungendo 2 mi dia 20 è 9.

Non mancano le risposte con … risultato secco senza spiegazione!

Quesito 2 geometrico

Questo ha dato, senza dubbio, più da pensare! A tutti, indistintamente, prima e seconda. Molti risolvono, fra aiutini in casa e intuizioni, ma non riescono a spiegare chiaramente il perché delle deduzioni o dei risultati. Spesso si è confuso il concetto di perimetro con quello di area.

Pubblico tuttavia tutte le risposte, anche imprecise, considero che il lavoro c’è stato. Anche quello delle mamme/babbi

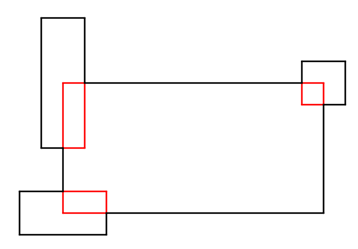
Si chiede la lunghezza del contorno disegnato a tratto spesso.

Vediamo:

Margherita (I):

Sapendo che 20 cm è la somma del perimetro dei rettangoli piccoli, faccio:
20÷4=5 cm, così trovo i lati che si trovano al interno del rettangolo iniziale poi:
20-5=15 cm [perché?].
Adesso, dal rettangolo iniziale (perimetro =30 cm) devo sottrarre la stessa quantità:
30-5=25 cm, e qui trovo i segmenti del rettangolo iniziale [perché?].
Infine sommo: 25+15=40 cm, che è il TOTALE.

Sofia:

il perimetro della figura è 40 cm. Ho diviso i rettangoli più piccoli in 4 parti: 1/4 di 20 cm, che è il perimetro complessivo dei 3 rettangoli, uguale a 5 [cosa trovi?]. I 5 cm li ho sottratti a 20 ottenendo 15 cm che è la misura totale delle parti grosse dei rettangolini [in quanto…?]. Poi a 30 cm ho tolto sempre 5 cm ottenendo 25 che è la misura delle parti grosse del rettangolone [ancora, in quanto… ?] Infine ho sommato 25 a 15 ottenendo 40 cm.

Stefano P., spiega con una sua figura:

Per calcolare il perimetro richiesto ho sottratto le parti in rosso dal perimetro formato dalla somma dei tre rettangoli più piccoli che è uguale a 20 cm: le parti in rosso sono uguali alla metà di questo perimetro 20 : 2 = 10 cm [anche qui bisognerebbe spiegare con chiarezza il perché, ma è più accettabile l’intuizione]
Se il perimetro del rettangolo grande è 30 cm, allora il perimetro dell'intera figura sarà 30+10 = 40 cm [e questo non è affatto chiaro, direi errato!].

Gabriella, riporto la soluzione anche se davvero poco precisa, si apprezza l’impegno:

per trovare il perimetro di un rettangolino con tratto sottile ho fatto 1/4 di 20 cioè 5 [qui si confondono i concetti perimetro-area, già la figura lo rivela]. Poi ho trovato il perimetro totale dei 3 rettangolini 5x3=15 [??], perché nel quarto angolo non c'era il rettangolino; 30-5=25 [perché?]; 25+15 = 40 perimetro totale della figura.

Buona invece la risposta di Antonio (I):

Secondo me la misura del contorno spesso può essere 40 cm. Sono arrivato a questo risultato perché ho notato che nei rettangoli piccoli manca 1/4 del perimetro in ogni rettangolo, quindi: 20/4 = 5 cm. Visto che ho dei rettangoli devo moltiplicare per 2 il 5 ottenendo 10 cm che sottraggo dalla somma del perimetro dei rettangoli piccoli e da quello del perimetro del rettangolo grande:
20-20/4 + 30-20/4 = 20 + 30 – 10 = 40 cm

I secondini:

Andrea:

Per prima cosa traccio le mediane [meglio, gli assi] dei rettangoli piccoli perché dividono in 4 il perimetro di ogni rettangolo [mmmh, insomma, non proprio. Dividono l’area in 4 parti! Come sottolineato, buona l’intuizione ma non la spiegazione]. Quindi 1/4 20= 5 cm che devo sottrarre a 20 cm e ottengo 15 cm. Sottraggo 1/4 20 cm anche dal perimetro del rettangolo grande, cioè 30 cm, perché essendo 3 rettangoli sottili da sottrarre devo raddoppiare la somma di un altezza e di una base e quindi 20 cm-5 cm+30 cm-5 cm = 40 cm, cioè il perimetro della parte evidenziata in rosso.

Paola, risposta simile a quella di Andrea ma, mammamia l’esposizione!

Michele:

Calcolo la somma totale del perimetro del rettangolo ABCD più il perimetro dei rettangoli sui vertici A, B e D, quindi: 30 cm + 20 cm = 50 cm. Da questa somma sottraggo la lunghezza del contorno sottile che misura 10 cm, perché osservando la figura, tale lunghezza equivale alla metà del perimetro totale dei tre rettangoli piccoli (20cm/2= 10cm).
Quindi sottraendo la lunghezza del contorno sottile (10 cm) ottengo la lunghezza del contorno spesso: 50 cm – 10 cm = 40 cm

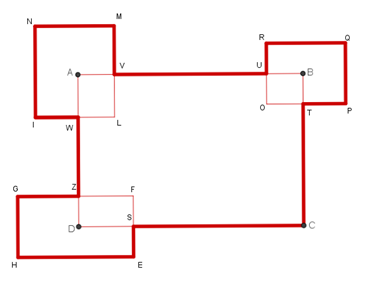
Luca, scompone la figura in segmenti

e correttamente afferma che (io sintetizzo per una più facile comprensione): due segmenti consecutivi, fra quelli a tratto sottile, rappresentano 1/4 di perimetro di ciascun rettangolo ai vertici. Quindi:
il perimetro esterno richiesto è dato dal perimetro del rettangolo iniziale meno le lunghezze di tre coppie di quei segmenti (1/4 20), a cui sommo il perimetro dei rettangoli con vertici in A,B,C, meno le tre coppie di segmenti uguali e paralleli alle prime (sempre 1/4 20). Cioè: 30 – (1/4 20) + 20 –(1/4 20) = 40 cm

Aurora, insomma insomma…:

il perimetro della parte rossa misura 40 cm.
Visto che la parte chiara è i 1/2 di 20 quindi 10 cm, non mi resta che fare 20-10=10 cm [e fino a qui, ok]. Poi, 30+10=40 cm. Aggiungo 10 a 30 perché la parte chiara del rettangolo è uguale a quella dei rettangoli più piccoli [No, direi che non è proprio chiaro, anzi direi che così non è!]

Marta C.:

Nella figura noto che i rettangoli a tratto meno spesso sono 1/4 delle tre figure a tratto più spesso [1/4 in che senso?] che hanno il loro centro nei vertici del rettangolo principale.
Sapendo che il perimetro dei tre rettangoli è di 20cm e quindi vedendo che i tre rettangoli a tratti più fine rappresentano 1/4 dei tre rettangoli con centro A B D: 1/4 di 20 cm=5 cm. Ottengo i rettangoli a  bordo meno spesso [NO], li sottraiamo al perimetro totale 30-5=25cm e poi lo sommiamo ai restanti 3/4 delle figure da 20cm di perimetro =15 cm; 25+15=40cm

Sara, soluzione come quella di Michele, altrettanto corretta (… ho trovato la misura dei segmenti chiari; per trovare il tratto spesso faccio 50 (20+30 somma del perimetro di ogni rettangolo)-10=40cm).

Uguale la soluzione di Roberta (30+20-5*2=40 cm; 5*2 è la somma dei perimetri dei rettangolini sullo sfondo, ottenuta notando che due lati consecutivi di ogni rettangolino [due lati per ciascuno quindi la loro somma] costituiscono 1/4*20 cm=5 cm).

La soluzione di Yuri è simile a quella di Marta C., con le solite imprecisioni/confusioni area-perimetro (i rettangolini a sfondo sottile sono 1/4 dei tre rettangoli con il centro nei vertici di ABCD [NO, quella è l’area]) Poi sottrae 5 cm da 30 e aggiunge i 3/4…

Antonio infine, risolve come Michele, Roberta, Sara. Non manca la poca chiarezza su quel 1/4!

Da ultimo, il

Quesito 3 riservato alle classi seconda e terza.

Risolvono per la seconda (noi quest’anno siamo I e II): Andrea, Paola, Marta C., Roberta, Michele, Yuri, Luca, Maria, Elisa, Sara, Aurora, Antonio, Valentina, Marta D.

Sintetizzo le risposte, tutte simili, tutti hanno individuato il triangolo rettangolo a cui applicare il Teorema di Pitagora:

La superficie dove poggiano i pannelli è di 16 m^2. Ho usato il teorema di Pitagora perché ho individuato un triangolo rettangolo di cui ho le misure dei cateti (3 m e 4 m, 4 m è il cateto parallelo e uguale a una dimensione del box auto). Quindi per trovare la misura della seconda dimensione della superficie dove poggiano i pannelli, che è l'ipotenusa del triangolo rettangolo, devo fare: $\sqrt{3^2+4^2}=\sqrt{25}=5 m$. La superficie della parte dove poggiano i pannelli si trova b*h = 3.2 m*5 m = 16 m^2.

Invano io ho commentato che mi aspettavo qualche guizzo d’ingegno! Oh, babbeozzi, il prof Davide direbbe babbani , chiedevo di riconosce la terna pitagorica 3, 4, 5! Avendo i cateti uguali a 3 e 4 unità l’ipotenusa non poteva che essere 5 unità.

Ora lo so che qualcuno dirà: l’ho riconosciuta ma pensavo chiedesse di applicare bene il Teorema di Pitagora - No, i guizzi son guizzi! E meglio averli e usarli!

Bene, mi pare di aver detto tutto anche stavolta. Segnalare eventuali mancanze.

Bravo come sempre a chi ha lavorato o a chi quantomeno ha provato.

Occhio ai nuovi giochi fra qualche giorno dal prof Davide. Ma anche qui la segnalazione.

Articoli correlati per categorie