Eccole,
le soluzioni del
Due a settimana …_17
Ancora una volta quesiti estremamente facili, sarà il caso di impegnare un po’ di più questi cari ragazzi? Solo appena appena, nessuno si spaventi!
Via le soluzioni.
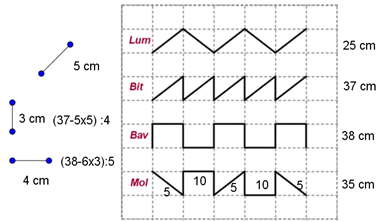
Quesito 1 le lumache e le tracce
Per la classe prima, i solutori: Margherita, Stefano P., Antonio, Ludovica, Stefano B., Sofia, Giorgia, Fabio.
Ragionamento e soluzione analoghi per tutti, trovano nell’ordine, la traccia-diagonale, l’altezza e la base dei rettangoli della griglia. Questi ultimi vengono chiamati anche lati minore e maggiore dei rettangoli oppure altezza e larghezza, insomma i concetti sono validi. Sintetizzando:
Ho iniziato a calcolarmi quanto era lunga la diagonale dei rettangolini partendo dal 1° percorso e ho fatto 25 : 5 = 5 dm.
Dopo mi sono calcolato, dal secondo percorso, l'altezza, facendo prima 37 - 25 = 12 dm (ho sottratto le 5 diagonali) e poi 12 : 4 = 3 dm.
Infine ho calcolato la larghezza dei rettangolini togliendo dal 3° percorso le altezze: 6 X 3 = 18 dm (6 altezze)
38 - 18 = 20 dm; 20 : 5 = 4 dm (5 larghezze)
Per calcolare il percorso di Mol ho fatto:
5 X 3 = 15 dm (3 diagonali)
3 X 4 = 12 dm (4 altezze)
4 X 2 = 8 dm (2 larghezze)
Mol percorre 15 + 12 + 8 = 35 dm
Sofia riporta su Geogebra lo schema della soluzione:
Per la seconda, solutori: Elena, i gemelli Paola e Andrea , che lavorano in rigorosa indipendenza eh, Roberta, Yuri, Davide, Aurora, Luca, Marta C., Antonio, Sara, Valentina, Elisa.
Le soluzioni ricalcano le precedenti, minime le varianti, diagonali, basi altezze, linee oblique, lati verticali e orizzontali, linee spezzate …
Roberta:
Ho notato che il percorso fatto da Mol è un misto tra quello di Lum, quello di Bit e quello di Bav.
Quindi ho preso come unità, da ogni percorso, i segmenti evidenziati
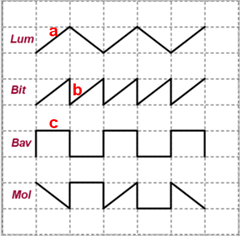
Da Lum → a = 25/5 = 5 dm
Da Bit → b= (37- a*5)/4 = 3 dm
Da Bav → c= (38- b*6)/5 = 4 dm
Mol = a*3 + b*4 + c*2 = 35 dm
Davide, senza parole:
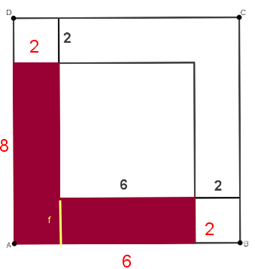
Quesito 2 area della L
Solutori prima
Margherita:
Ludovica:
prima area, rettangolo orizzontale: 6*2=12
seconda area, rettangolo verticale: 8*2= 16
16+12=28 [Ehi, cominciamo ad usare le unità di misura!]
Antonio:
L'area della L colorata, secondo me, è di 28 cmq.
Ho calcolato l’area del quadrato piccolo: 4 cmq (lxl=2x2), poi ho calcolato l'area del quadrato medio (6x6=36cmq).
Per calcolare l'area del quadrato grande mi serviva la misura del lato che ho ottenuto sommando il lato del quadrato piccolo più quello medio (6+2) più il lato di un altro quadrato piccolo (2) ottenendo un lato di 10 cm.
Quindi l'area del quadrato grande: 10x10= 100cmq.
Per trovare l'area della L colorata ho tolto dal quadrato grande l'area di quello medio e di due piccoli (100-36-4-4=56cmq)
che poi ho diviso per due visto che rimangono due L:
56:2=28 cmq l'area della L colorata
Stefano B: stessa soluzione-Antonio
Stefano P.:
Per calcolare l'area della L mi sono calcolato prima l'area di un quadrato da 8 cm di lato, che ho ottenuto facendo la somma tra il lato da 6 cm e quello da 2 cm. Quindi: 8x8=64 [cmq!]. Da questa ho tolto l'area del quadrato da 6 cm di lato (6x6 = 36): 64 - 36 = 28 [cmq!]
Quindi l'area della L misura 28 [cmq!]
Sofia:
per trovare l'area della L ho diviso la lettera in 2 rettangoli e visto che l'area del rettangolo si calcola base x altezza, ho fatto: per
il rettangolo alla base 6x2=12, per quello in verticale 8x2=16 quindi 12+16=28, l'area della L è 28. [mi sono stancata di aggiungere le unità di misura. Perdonati solo per stavolta!]
Fabio:
Per la seconda, i solutori:
Paola:
Per trovare l'area della "L" bisogna prima trovare l'area degli altri quadrati quindi faccio 6*6 = 36 cm^2 [quadrato interno] e 6(+2)*6(+2) = 8*8 = 64 cm^2. Quindi: 64 - 36 = 28 cm^2
Andrea:
L’area della "L" misura 28 cm^2 e ho 3 soluzioni per trovarla:
1) la si può trovare calcolando l'area di uno dei quadratini piccoli che è 4 cm^2, e trovare tanti quadratini quanti sono dentro la "L" e io ne ho trovato 7;
2) la misura si può trovare anche con un’espressione: [10*10-(6*6+2*2*2)]:2= 28 cm^2;
3) la misura si trova anche tracciando un quadrato immaginario (!) da 8 cm di lato, trovando l'area e sommando l'area dei due quadratini da 4 cm^2 di area, trovando 72 cm^2, che viene sottratto a 100 cm^2, che è l'area del quadrato grande e otteniamo 28 cm^2 che è la misura dell’area della "L".
Roberta: soluzione L suddivisa in due rettangoli.
Elena: soluzione 2-Andrea (discorsiva, non con espressione)
Luca [non esistono le unità di misura!]:
prima soluzione:
Per risolvere questo quesito ho considerato l'area totale del quadrato grande di lato pari alla somma di 2+6+2=10
(6 e 2 sono i lati dei quadrati costruiti all'interno):
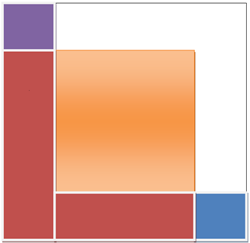
A= 10*10=100
quindi calcolo le aree dei quadrati costruiti all'interno:
A1= 2*2=4 area quadrato di lato 2
2*A1= 8 area totale dei due quadrati di lato 2
A2= 6*6=36 area quadrato di lato 6
quindi:
A-(2*A1 + A2)= 100 - (8 + 36) = 56 che rappresenta l'area delle due L presenti all'interno della figura,
l'area cercata sarà la metà di 56
A "L" = 56 :2 = 28
seconda soluzione:
Ho calcolato l'area dei due rettangoli in cui posso suddividere la figura a forma di L:
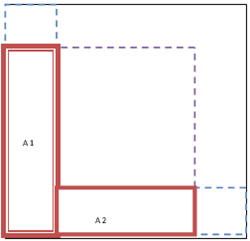
un rettangolo ha altezza pari a 6+2 = 8 e base pari a 2, la sua area è A1= 8*2=16
un rettangolo ha altezza pari a 2 e base pari a 6, la sua area è A2= 6*2=12
L'area totale della L sarà: A1+A2 = 28
terza soluzione:
considero l'area L divisa in due rettangoli e un quadrato,
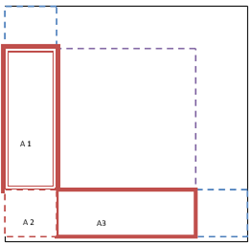
A1 = A3 = (6*2)=12
2 *A1 = 12*2 = 24 area complessiva dei due rettangoli di lati 6 e 2
A2 = 2*2 = 4 area del quadrato di lato 2
A “L” = 2*A1 + A2 = 24 + 4 = 28
Yuri: soluzione1-Luca
Marta C.: soluzione1-Andrea [nessuno dei due spiega però, dimostra, che Il quadratino con area 4 è contenuto nella L 7 volte]
Antonio: soluzione due rettangoli…
Aurora: anche, soluzione due rettangoli
Davide: soluzione due rettangoli uguali e un quadrato (“d’intersezione” lo chiama, ok)
Valentina, Elisa e Maria mi danno la soluzione su foglietto, soluzione due rettangoli.
Sara:
a ogni angolo del quadrato corrisponde un altro quadrato che ha il lato di 2 cm quindi con un'area di 4 cm quadrati. Il quadrato al centro ha il lato di 6 cm e quindi quello di 3 quadrati piccoli.
La "L", contando i 3 quadratini contenuti in ciascun "braccio" e il quadratino nell'angolo, è composta da 7 quadratini ciascuno con un'area di 4 cm quadrati, quindi l'area della "L" si calcola facendo 4x7= 28 cm quadrati.
Quesito 3 ancora quadrato ma da dissezionare e ricomporre!
Hanno costruito, ritagliato, ricomposto … Bravi! Seguono tutte le foto…
Per la prima, i solutori e le soluzioni:
Stefano P.:
Margherita (con la croce non ci siamo):
Antonio (Anto, fai foto più decenti! ):
Stefano (per non parlare delle tue, Ste’):

Sofia:
Fabio:
Per la seconda:
Roberta:
Robi fa una considerazione:
se una figura viene scomposta in varie parti e ricomposta variando la posizione delle parti, l'area è sempre la stessa.
[I due quesiti sulle aree ci servono - già li usiamo …- per parlare di equivalenza di figure piane]
Luca (oddio le foto…):
Paola (ah, qui proprio belle … ):
Andrea (uuhh!!):
Antonio (io non commento più!)
Aurora (che inoltre… cura gli sfondi, soprattutto della croce ):
Davide (ma si può così…? e io accetto….)
Yuri (no, non c’è da pensar male… sono stata informata, Yuri e Davide hanno usato, casualmente, carta dello stesso colore. Chissà chi ha pensato male! ):

Sara, descrive come ha costruito, direi un po’ impegnativo da seguire, ma non invia foto!
Bene, avrò riportato tutto/i? Avvertitemi in caso di sviste.
Solite lodi a chi ha lavorato, qualcuno non ha potuto per motivi tecnici (e io non avevo capito bene la situazione..), e a chi ha fatto del suo meglio!
Prossimo appuntamento, dal prof Davide!








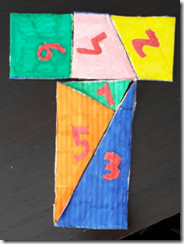





















































La prima parola che mi sia affaccia alla mente è abbondanza. Che abbondanza!
RispondiEliminaLe immagini, ad esempio: un profluvio di immagini.
Soprattutto le foto del terzo quesito danno l’idea di una partecipazione vivace e abbondante. Bello! Mette allegria!
Poi, detto tra noi, mi rincuora notare che anche qui l’uso delle unità di misura fatica a prendere piede. Pensavo di essere l'unico insegnante in Italia a rodersi il fegato sui cm non scritti. :-)
Di nuovo "bravi!" a tutti i solutori.
Ci vediamo prossimissimamente per una nuova tornata di giochi. Natalizi, ovviamente.
Grazie prof. Foto abbondanti, colorate sì ma allegre non saprei. Ok è quasi Natale e non dobbiamo essere tristi :-)
RispondiEliminaLe unità di misura: spero di aver sottolineato abbastanza. Mi sento anch'io rincuorata :-)
Aspettiamo i giochi natalizi!!