Ragazzi, II,
ho da proporvi ancora un’interessante attività sui punti notevoli del triangolo.
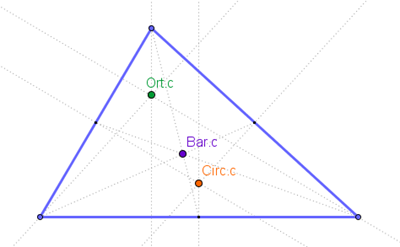
Osservate la figura sotto. Ho preso in considerazione solamente l’ortocentro, il baricentro e il circocentro. Potete intravedere perpendicolari, mediane e assi dei lati. Ma sapete fare la costruzione!
La domanda è: riuscite a scoprire una correlazione tra i 3 punti? Una caratteristica che li accomuna?
E anche: in che rapporto stanno le distanze tra i punti?
Sull’applet che andrete ad aprire, agite sui vertici del triangolo per modificarne la forma, osservate con attenzione i tre punti: cambiano le loro posizioni ma... c’è un’invariante! Utilizzate gli strumenti di GeoGebra, provate qualcosa!
Se proprio non doveste riuscire, vi darò degli indizi per la ricerca...
Ma ora cliic! Su, a sperimentare!
Se volete, comunicate nei commenti le vostre scoperte o solo eventuali osservazioni, considerazioni, richiesta di chiarimenti o quant'altro!
[Aggiornamento]
Ebbene, caro Marco, stamane attività in classe!
giacché nessuno aveva letto il post ...
Abbiamo lavorato tutti insieme direttamente su GeoGebra (con la LIM). Veronica, e Bachisio, aiutati un po’ da altri, hanno costruito l’ortocentro, il baricentro e il circocentro.
Abbiamo nascosto gli oggetti superflui ai fini dell’attività e lasciati in evidenza solo i tre punti.
Mio invito all’osservazione mentre si muovono i vertici del triangolo e se ne varia la forma: possiamo dire qualcosa sui tre punti?
Da più parti si mormora: sono allineati. Qualcuno è invitato a tacere per dare spazio ...
Letizia nota però che il baricentro è il punto che rimane sempre al centro, tra il circocentro e l’ortocentro (e naturalmente è l’unico punto sempre interno al triangolo, ma questo già si sapeva)
Si torna all’allineamento: Gabriele, Francesco (e altri) dicono che si può costruire la retta passante per i punti. Naturalmente bastano due punti per definire una retta e infatti lo strumento di Geogebra è Retta per due punti. Si decide di farla passare per l’ortocentro e il circocentro.
Questo forse rassicura... ma l’insegnante (“diabolica”, Marco) chiede: ma come faccio ad essere certa che anche il baricentro è un punto della stessa retta?
Oh, ma presto detto...
Letizia: ma c’è lo strumento.
- Cioè? (da noi mai stato utilizzato, lo sottolineo ...)
E’ Relazione tra due oggetti 
Ok, Letizia fa clic sul baricentro e sulla retta e:
e brava Leti!
Ma c’è ancora Erica, che ha notato dell’altro.
Che volevi dire Erica?
- Volevo dire che la distanza tra ortocentro e baricentro è doppia di quella tra baricentro e circocentro.
Io sto per guardare male Erica: ma questi qua mi rubano le domande!
Naturalmente sono invece felicissima e mi complimento con Erica per l’occhio! Misuriamo le due distanze con Geogebra e... Erica ha ragione! (in figura i tre punti sono indicati con la relativa legenda, i nomi dei punti sono diversi)
Ora io armeggio con un vertice del triangolo e...
Cosa cerco di fare, ragazzi?
- Vuole far coincidere i tre punti
E in quale caso i tre punti coincideranno?
- Quando il triangolo è equilatero.
riusciamo a ottenere uguali a zero le distanze:
ok, bravi...
Ma, ma ...io insisto:
Che mi dite però della retta nel caso del triangolo equilatero?
Qui occorre qualche minuto di riflessione in più, qualche osservazione - guida in più.
Francesco dice: la retta passa per tre punti ma sembra passare per un solo punto!
I tre punti ora coincidono, quindi passa per un unico punto.
Ragazzi, dovete utilizzare informazioni che già avete!
Dopo qualche istante, Letizia, senza scomporsi, come suo stile: per un punto passano infinite rette.
Benissimo! Dunque la retta (di Eulero) non è definita nel caso del triangolo equilatero.
Oh, ho scordato di dire che prima dell’osservazione sul triangolo equilatero, ho detto ai ragazzi che la correlazione tra i tre punti notevoli è stata studiata da un grande matematico del ‘700, svizzero, che voi conoscete bene, o se lo conoscete! (ma ai ragazzi non cito mica post e lavori... Solo in un secondo momento li ricordano loro)
Ebbene: Gabriele, trova che si tratta di Eulero.
E a Gabriele viene pure in mente che mentre cercava in rete sui punti notevoli, da qualche parte ha letto della retta di Eulero!
- Insomma ho rischiato anche stavolta che Gabri mi soffiasse la lezione! Ma uno stupendo rischio, no?























Nessun commento:
Posta un commento
I vostri commenti sono graditissimi, l'interazione è molto utile!
Non ci piace però comunicare con "anonimi". Vi preghiamo di firmare i vostri messaggi.
Come fare:
Cliccare su Nome/URL.
Inserire il vostro nickname nel campo "nome".
Lasciate vuoto il campo URL se non avete un blog/sito.
Grazie!